第一次听说《An Introduction to the Mathematics and Methods of Astrodynamics》这本航天动力学最经典的教材，是在本科 Orbit Mechanics 这门课上。后来费了很大力气找到了电子版，一看 800 多页，旋即放弃。假期从图书馆找到了中文译本，打算好好啃一啃这本书。

（本书封面）

（中文译本）

（作者 Battin）

（老师的 PPT 截图）

本文的价值（读了之后你能收获什么）

• 本文并不是对书本内容的简单搬运，事实上，本文是在解答作者留下的习题
• 所以，可以收获一份习题答案
• 当然，只做题是不够的
• 所以，在文末我对比了连分式展开和 Taylor 展开的精度
• 还有，即使书本的作者已经非常严谨，但还是被我找到一处笔误（几位译者也没发现）

提示

• 既然是习题答案，所以文风活泼（严肃）且生动（枯燥）
• 只要懂 Taylor 级数就能读懂本文
• 通篇都是长公式，所以，推荐横屏阅读（最好在大屏设备上阅读）

的连分式展开（习题 1-9）

Taylor 展开：

不妨令 （事实上， 时根本没有展开的必要，），两边同时除以 ，得

由超几何函数的定义

可以看出

根据高斯连分式展开定理（先拿来用，后面再证明）

其中，对

换句话说，奇偶项的系数的表达式是有区别的。

当 ， 时

此时，做一个恒等变形

继续展开下去，对于奇数项

对于偶数项

即

因此， 的连分式展开为

高斯连分式展开定理

引理（习题 1-3）

对 ，记 的偶数项和奇数项分别为

那么

因此

和

换句话说，奇数项减去它前面的偶数项为

偶数项减去它前面的奇数项为

则

记

有

或者

因此

对于超几何函数，令 ，则

且 时， 和 退化为

最终

换元，用 替换 ，得到高斯连分式展开定理

其中， 和 的表达式上文已经给出过。

的连分式展开（习题 1-10）

Taylor 展开：

时，两边同时除以 ，得

当 ， 时

此时，做恒等变形

继续展开下去，对于奇数项

对于偶数项

即

因此， 的连分式展开为

前面 的连分式的奇偶项不好合并，但是 的连分式奇偶项可以合并成

引入一个记号（本文结尾部分会用到）

的连分式展开（习题 1-10）

Taylor 展开：

把 的 替换为 ，整理后得到

的连分式展开（习题 1-11）

引理

引理的证明（习题 1-1）

几何级数

两边取 次幂，并二项式展开

换元，用 替换

以上二式相加、相减得到

和

令

则

令 ，得

两式相比

得证

当 ，， 时

故

继续展开下去，对于奇数项

对于偶数项

即

故

即

汇合型超几何函数的连分式表达式（习题 1-12）

称

为汇合型超几何函数。则

其中

书上的 漏掉了负号，给我造成了很大的困惑，如何证明加了负号是对的：

令上式 ，并做变量替换，用 替换 ，有

其中

进一步，做恒等变形

继续展开下去，对于奇数项

对于偶数项

即

的连分式展开（习题 1-13）

有

故

奇数项

偶数项

在偶数项分子分母同除以 ，还可以进一步简化

化简后的奇数项

化简后的偶数项

即

的连分式展开（习题 1-14）

定义

则

其中

做恒等变形

的连分式展开（习题 1-15）

已知

则

的连分式展开（习题 1-15）

已知

则

结尾

最后，研究一下连分式展开和 Taylor 展开的精度对比。前面已经给出了 的连分式展开和 Taylor 展开，注意到

因此， 的连分式形式和 Taylor 级数形式分别为

借助数学软件Mathematica。分别对二者从 1 阶展开到 40 阶，数值运算的精度设为 80 位精度，比较 的近似值与精确值的误差，并对误差取常用对数（以 10 为底），代码如下

结果如下图

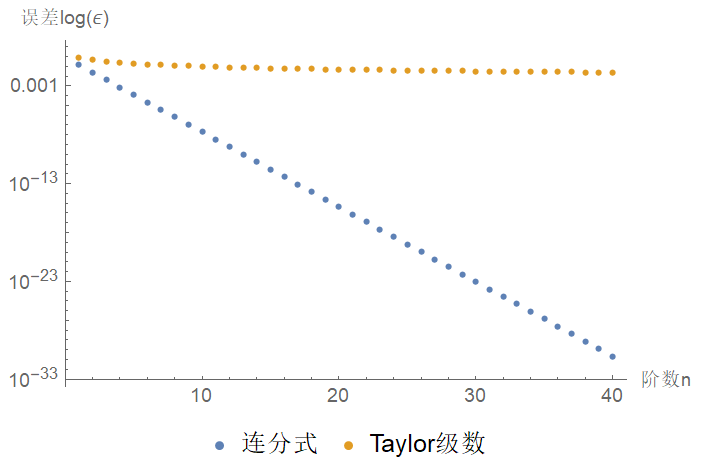
可以看出，随着展开阶数的增加，连分式的误差呈指数衰减，而 Taylor 级数的误差只是线性衰减。事实上，想要得到 的近似值 ，连分式只需展开到 15 阶，而 Taylor 级数需要展开到第 50000 阶，所以难怪作者 Battin 吐槽说：

连分式展开在大学课程中也没有获得应有的地位，尽管事实上连分式表达式在计算经典函数时远比人们更熟悉的无穷幂级数有效率：与级数相比，连分式通常收敛更快，收敛域更广。更具有讽刺意味的是，人们在发明幂级数前其实已经使用了上百年连分式。

但是，前面毕竟只是个例，下面在 区间上对 的连分式展开和 Taylor 展开进行对比，连分式展开到 10 阶，Taylor 展开 18 阶。由于Mathematica对 的计算精度有限，所以不再指定数值运算的精度。代码如下

结果如下图

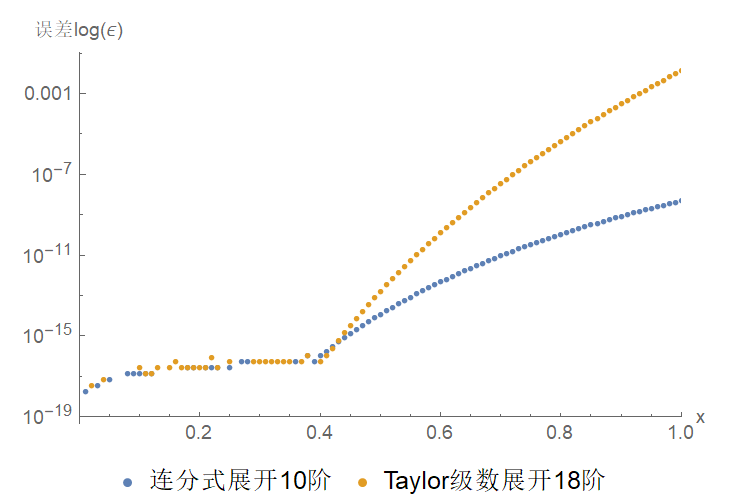
整体来说，连分式展开比 Taylor 展开精度更高，而且避免了大量的幂运算（由于数值计算的精度有限， 区间的误差结果并没有参考价值）