欢迎光临青崖同学的博客!!!

先祭出人畜无害的表情包一张↑，防止挨揍，鸽了一个月属实是身不由己，哈哈哈哈哈哈~~

---

另外，这是本年度最后一次更新惹，写完打烊！准备过年！

小学数学题

很久很久以前看到过一张动图（出处已经忘记了）：

玻璃板的开槽形状是双曲线。初次看到时，我一方面惊讶设计者的脑洞，另一方面很不理解背后的数学原理。前几天（严谨来说是 2021 年 8 月 4 号）看到博主 Matrix67 分享的小学数学题：

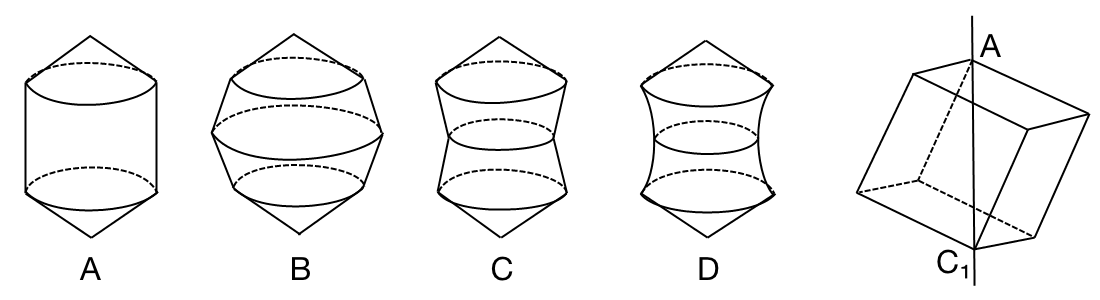
将一个立方体绕着它的对角线 旋转一周，会得到下面的哪一种立体图形？

迟疑 0.99 秒之后，我意识到这道题和上面的动图不是一回事嘛，都是一条直线绕它的异面直线旋转的问题，所以果断选 D。然而我还是想搞清楚背后的数学原理。

数学原理

不妨把动图里的装置抽象成下面的模型：

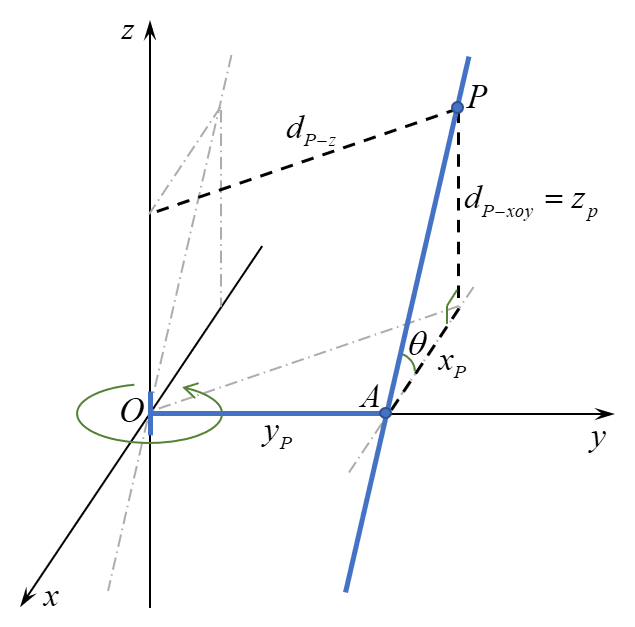
空间里有两条异面直线，我们希望构造空间直角坐标系 来描述它们。把其中一条固定不动并当作 轴，不妨称为“固定直线”。另外一条绕 轴旋转，不妨称为“旋转直线”。 轴的方向需要使得 平面与旋转直线平行（这样的 轴方向肯定能找到的）。原点 需要使得 轴与旋转直线相交（这样的原点 肯定也能找到），并记交点为点 。

到此已经把空间直角坐标系 构造出来了（当然还有其他的构造方法，上面这种相对好处理）。旋转直线与 平面的夹角记为 ，在旋转直线上任取一点 ， 点的坐标记为 。我们比较关注两个距离， 点与 轴的距离 ， 点与 平面的距离 ，因为这两个距离在旋转过程中始终保持不变。可以用 点的坐标表示这两个距离：

两式联立，消去 ，得到：

即 与 满足双曲线的方程。在此之后，有两种方法得到单叶双曲面的方程：

法一：

① 对于选定的 点，在旋转过程中 与 不变，即旋转过程中 与 始终满足双曲线的方程。

② 另外，双曲线方程只与 和 有关，而旋转直线上的任意 点的 和 都是相同的，由 点的任意性，对整条直线， 与 始终满足双曲线的方程。

综合以上两点，已经可以感觉出这是双曲线旋转形成的双曲面了。但是，这不算严格证明。

上面已经说明了 与 与旋转过程无关，那么不妨简化一点，就研究 点经过 平面时的情况，此时 ，所以双曲线方程退化为：

说明在旋转过程中，在 平面留下一条双曲线的轨迹（这就把一开始的动图解释了），如下图所示：

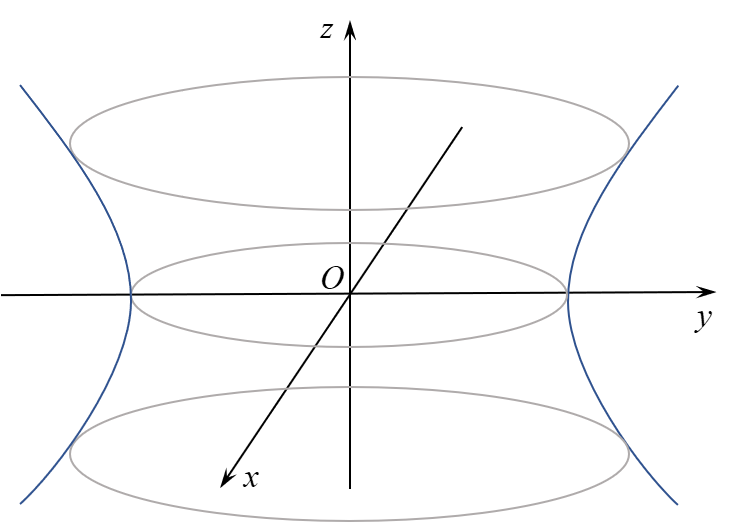
由几何知识，这条双曲线绕 轴旋转形成的是单叶双曲面，且方程为：

法二：

总感觉法一的说法过于啰嗦且欠点火候。其实，把

代入 与 所满足的双曲线方程，就可直接得到单叶双曲面的方程：

---

在 Mathematica 里把旋转的效果演示一下（这个动图我其实非常满意）：

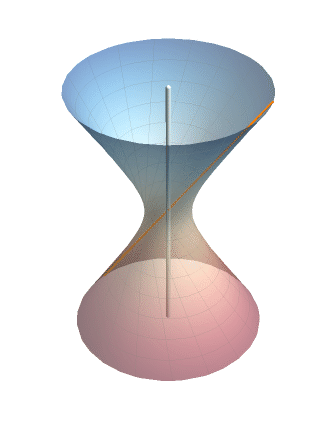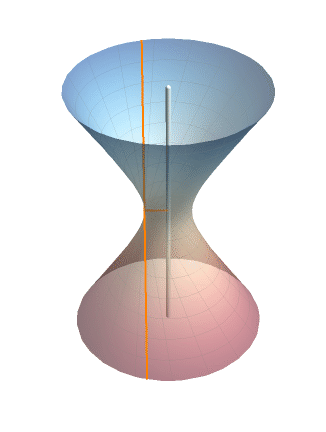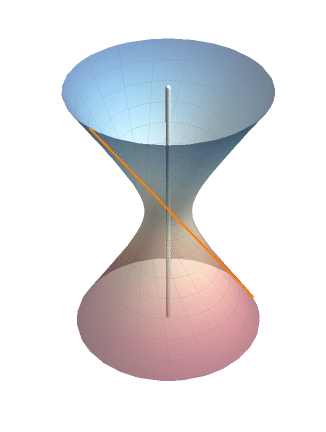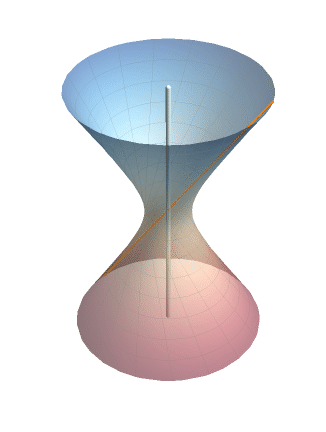
老规矩，上代码：

---

从上文的推导过程可以看出，单叶双曲面不仅可以由双曲线旋转产生（左图），还可以由一条直线绕它的异面直线旋转产生（右图）。

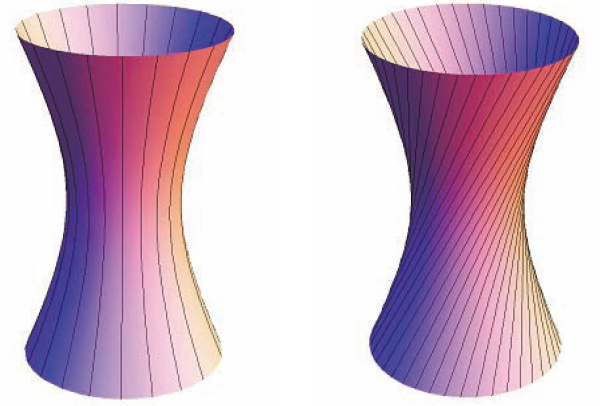
在 Mathematica 数学动图欣赏（一），我们曾经提到过单叶双曲面，就是这个原理。

著名的广州塔就是单叶双曲面建筑，从下图的视角可以清楚的看出钢柱是直的：

---

下面研究单叶双曲面的参数方程。当 与 轴重合时（不妨称为“基准位置”），把 点坐标表示成 ，其中 表示 点和 点的距离， 是常数表示 的距离。利用旋转矩阵表示从基准位置旋转角度 之后的 点坐标：

由此引出直纹面的概念。

直纹面

直线在空间中连续移动，扫过的曲面称为直纹面（单叶双曲面就是一种典型的直纹面）。把直线表示成：

直线连续移动时， 和 在连续变化，所以扫过的曲面可以表示成：

把上式和 点坐标进行对比，发现对于单叶双曲面，准线方程为：

母线的方向为：

除了单叶双曲面，双曲抛物面和莫比乌斯环也是直纹面。

双曲抛物面

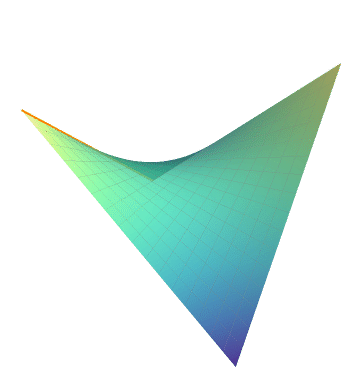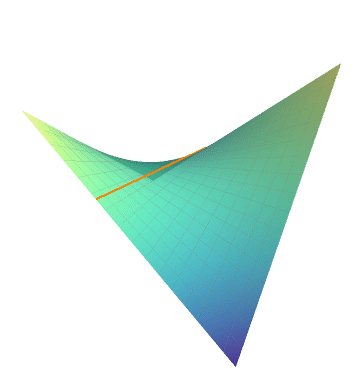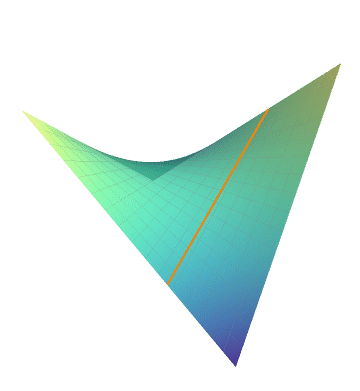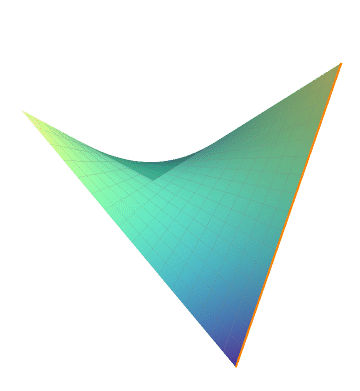
代码：

莫比乌斯环

代码：

结尾

最后，让我们回归到那道小学数学题上面，我把 Matrix67 博客里的动图复刻了一下：

既然是复刻别人的，自然要把代码公布出来：

trans[g_] := GeometricTransformation[g, RotationMatrix[{{0, 0, 1}, {1, -1, 1}}]];
c = trans[{Pink, Cuboid[{-0.5, -0.5, -0.5}]}];
c0 = trans[{Thin, Line[{{0.5, -0.5, -0.5}, {0.5, 0.5, -0.5}, {0.5, 0.5, 0.5}, {-0.5, 0.5, 0.5}}]}];
cEdge = Graphics3D[Table[Rotate[c0, t, {0, 0, 1}], {t, 0, 2 Pi, Pi/20}]];
draw[t_] := Show[{Graphics3D[Rotate[c, t, {0, 0, 1}]], cEdge}, Boxed -> False, PlotRange -> 0.9 {{-1, 1}, {-1, 1}, {-1, 1}}, ViewPoint -> {Infinity, 0, 0}, Lighting -> "Standard"];
Manipulate[draw[t], {t, 0, 2 Pi, Pi/4}]

结尾之结尾

本年度最后一次更新，打烊惹！

从夏木阴阴、到秋叶初丹、再到摇落蹉跎，季节的更替恰好契合了开学以来三个月的状态变化，也象征着博文的产出越来越少。写博客确实改变了我很多，这个过程中我认识到我不喜欢知识，我只是喜欢学习新知识，喜欢那种从无到有、从陌生到熟悉的感觉，真正学会之后反而兴致全无了（我以为这种心理很独特，不过后来发现许多博主都这样嚯）。

🧡🧡🧡感谢这个半私密的小天地带给我的欢喜🧡🧡🧡