设想一下有一些单项式，应该按照什么准则对它们进行排序？这是一个很现实的问题，因为书写它们的时候总得有个先后次序吧。为了便于叙述，记单项式为 ，其中 为变量， 为常量，不难发现 的次数为 。

单项式的种类数

在探讨排序之前，有必要知道这种变量数为 、次数为 的单项式的种类数 是多少？

以 ， 为例，通过枚举可以写出：

共 10 种，所以 。

注：虽然书写时省略了 0 次方，但这并不代表它们不存在。

分成以下三种情况讨论：

• Case 1: 当 时，意味着不存在变量，这种情况无意义，即
• Case 2: 当 时，意味着只有 一种情况，即
• Case 3: 当 且 时，把向量 的最后一个元素 分离出来，得到新的向量 。用 构造单项式，次数为 的单项式通称为 ，则可把 分为如下 类：

那么 自然等于这 类各自的种类数相加，即

简单验证一下：

对上式作变量替换，用 替换

惊喜地发现

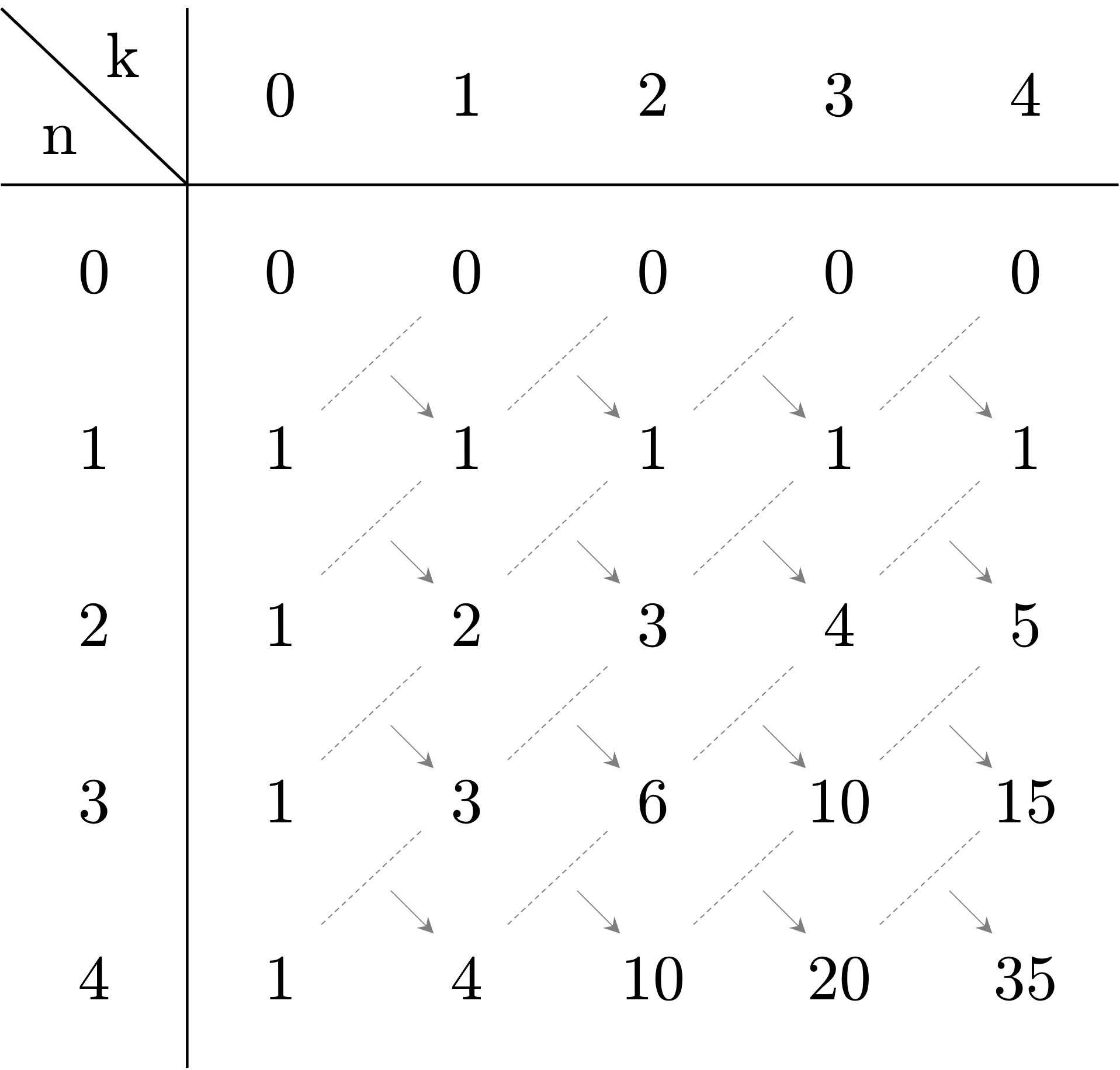
根据这个关系，可以构造一张表格。

---

先把 Case 1 和 Case 2 在表格上表示出来：

对于 Case 3 来说， 在 的上侧， 在 的左侧，示意图如下：

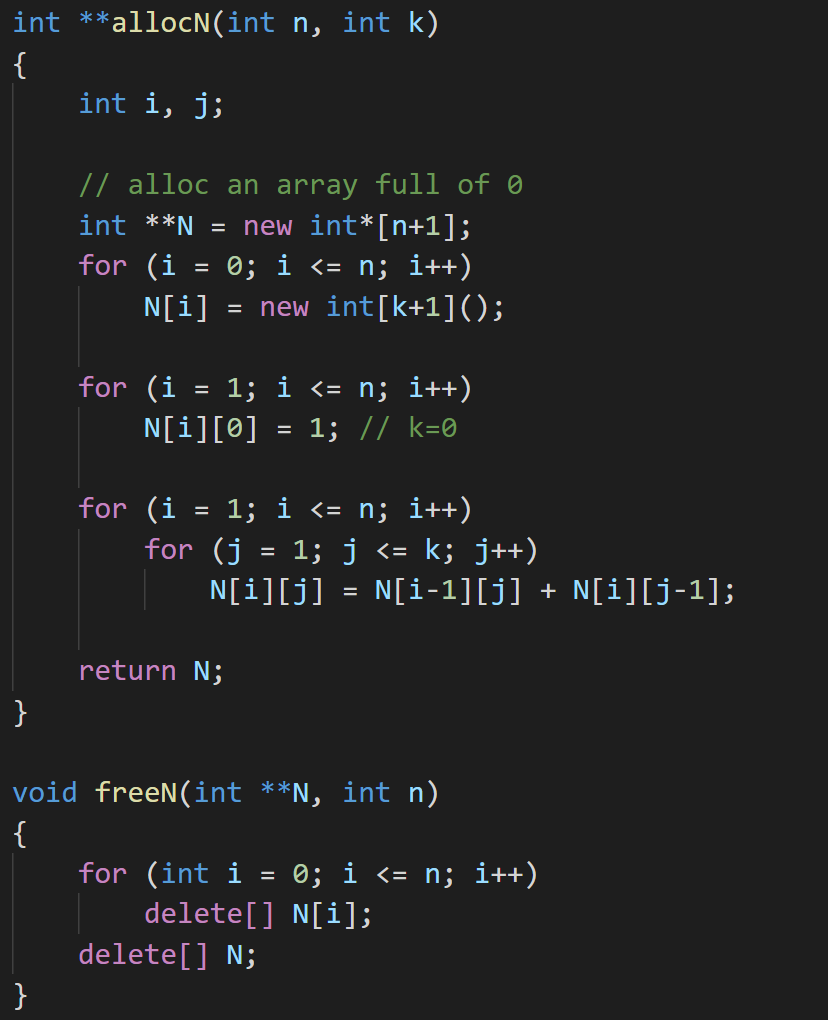
用 C++ 实现以上过程：

这个表格中蕴含着贾宪（杨辉）三角形：

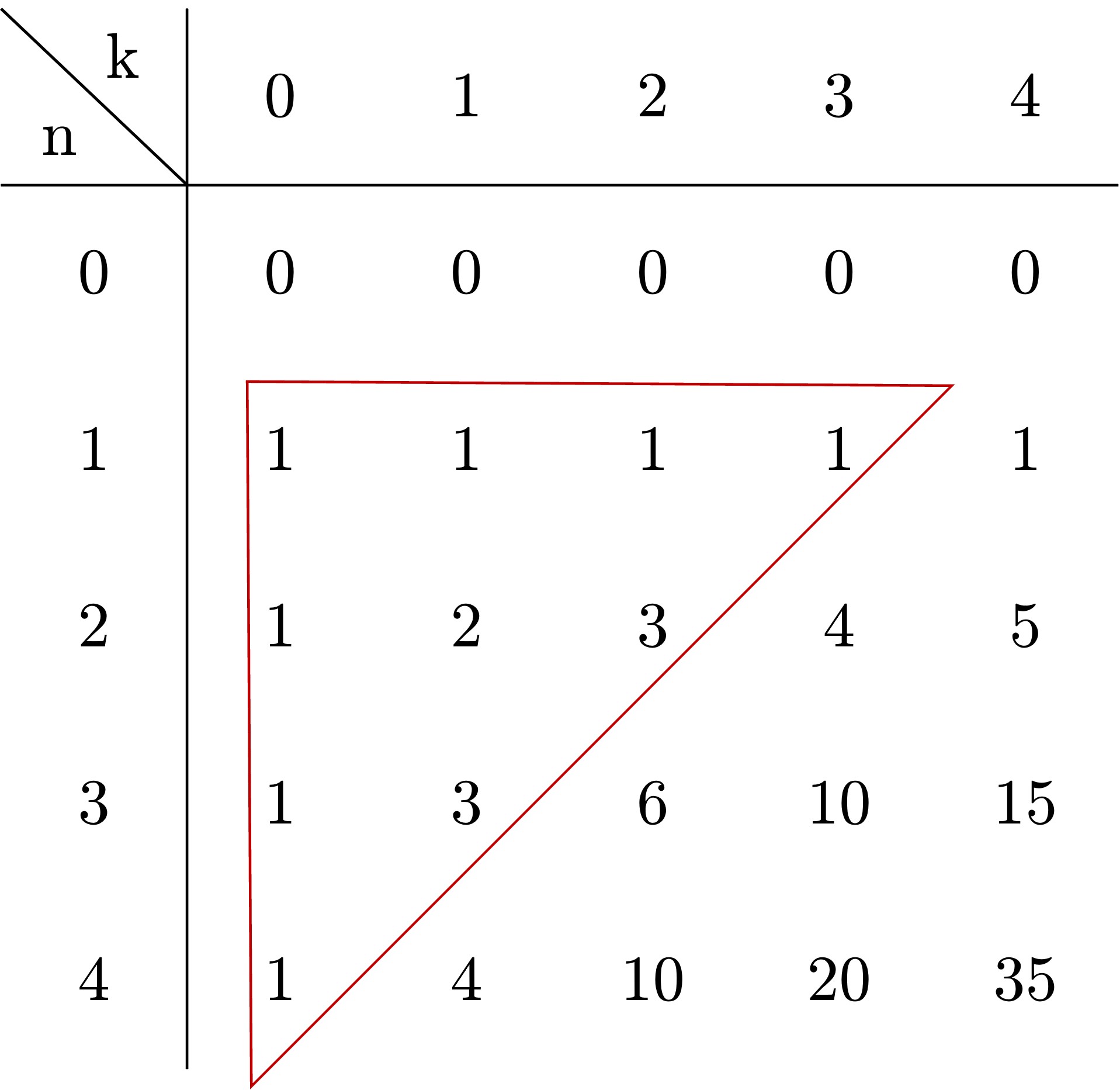
如果想要计算任意位置的 ，每次都需要列表很麻烦，那么 有没有通项公式呢？有的，我们直接给出结论：

其中，组合数 还有另外一种写法 。

可以用数学归纳法进行证明：

• 当 时，对任意的 ，都有 成立。
• 当 时，假设对任意的 ，都有 成立。
• 证明当 时，对任意的 ，都有 成立，即可

得证。

备注：上式最后一个等号利用了朱世杰恒等式：

我们探讨了单项式的种类数问题，直接给出了通项公式，并用数学归纳法进行了证明。但是数学归纳法只能证明，却不能告诉来历。既然通项是组合数的形式，那么 很可能具有组合意义，我们尝试从组合数学的角度理解一下。 代表着方程 的自然数解的个数（因为 是单项式的次数），用组合数学里经典的隔板法就可以直接给出结果了。

• 先考虑 的正整数解的个数。这一问题等价于 个小球用 个隔板隔开，每个区域至少一个小球。比如：

问题又等价于从 个小球间隔中选 个放隔板，答案一目了然，为 。

• 再考虑自然数解的情况。 等价于 ，那么 的自然数解个数等价于 的正整数解个数，为 ，得证。

朱世杰恒等式

结合表格，当 时，有

当 时，有

当 时，有

上一行的前 项和是下一行的通项。以上过程实际上就是朱世杰（1249 年－1314 年）的垛积法的核心思想。垛积法出自朱世杰的著作《四元玉鉴》（1303年）。所谓垛积，即堆垛求积，研究某种物品按一定规律堆积起来求其总数问题。

• 对应茭草垛，即把茭草捆扎成束，进行堆垛，每层比下层少一束，求总和。

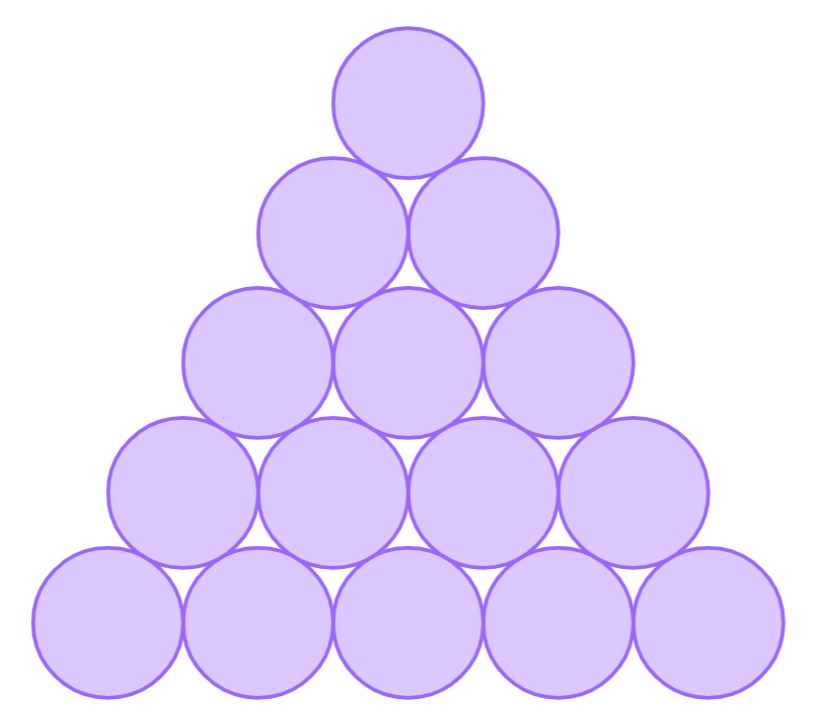
• 对应三角垛，可以用果子举例，每一层的果子按照茭草垛来排列，从最上层开始每层果子数为

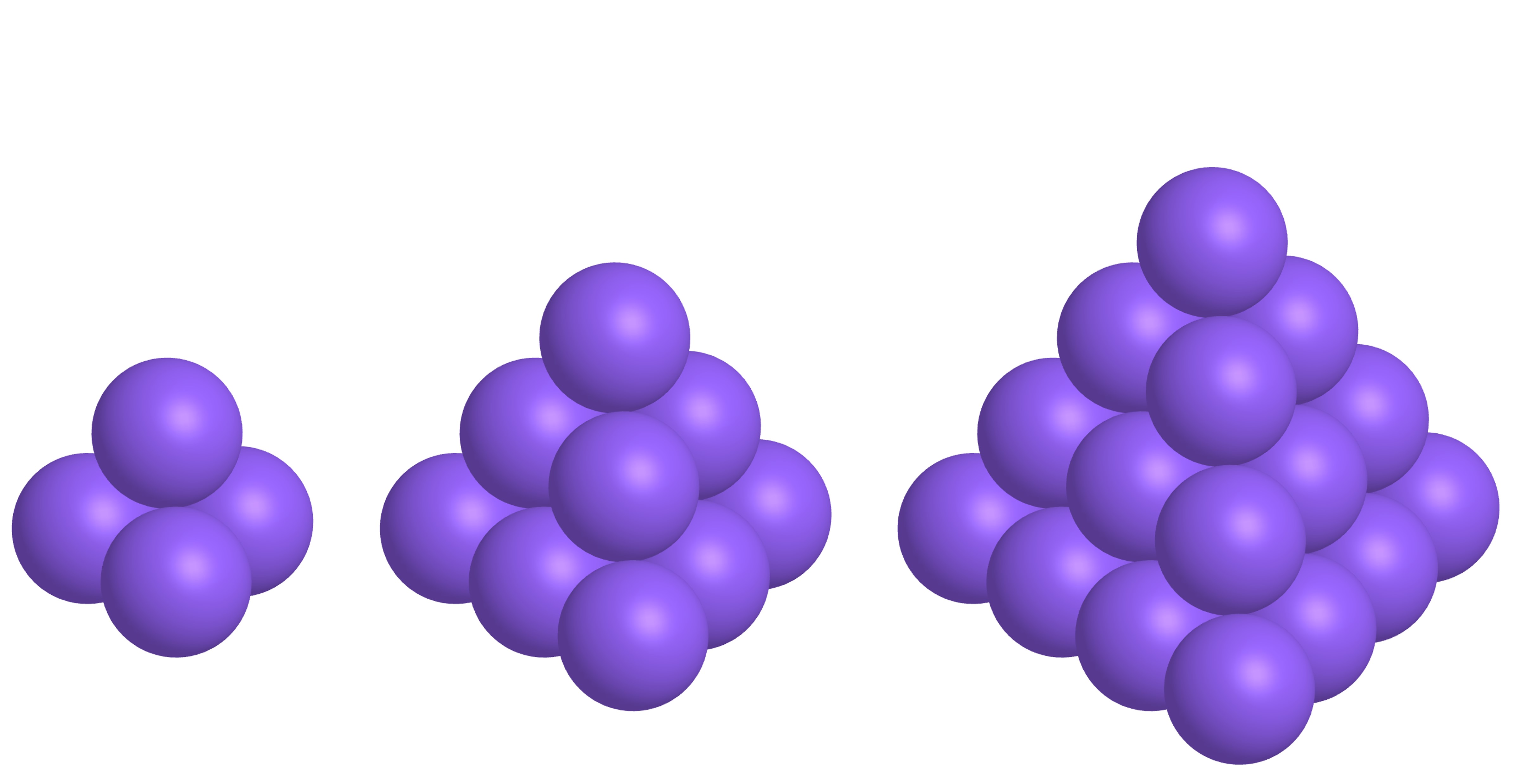
有实物演示如下：

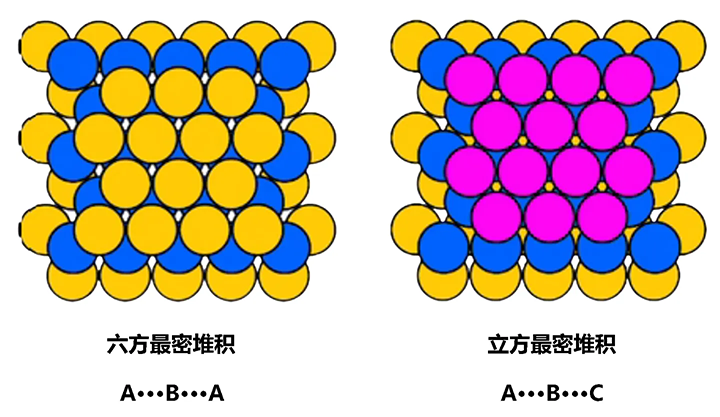
这种堆积形式还叫作面心立方最密堆积，空间利用率为 ，是空间最密的堆积方式之一。金、银、铜等金属的晶胞是这种结构，在高中化学《物质的结构与性质》中曾介绍过（当年对这些信手拈开）。至于为何是空间最密的堆积方式“之一”，因为还有一种六方最密堆积和它的空间利用率相同：

• 对应撒星形垛，还用果子举例，从最上层开始每层果子数应为 但是，撒星形到底是什么形状，我没有找到任何有关的描述，它还有一个名字叫做『三角更落一垛』。有一种较为合理的可能，它对应四维空间的堆积问题（而且有可能是四维空间的最密堆积）。不妨类比一下，所谓茭草垛其实对应着『平面圆形最密堆积』，三角垛对应着『立体球体最密堆积』，那么撒星形垛是否对应着『四维超球最密堆积』？

对于平面最密堆积到立体最密堆积升维的过程，平面之外的那个维度上的层与层，投影回平面后，有一种关系，即下层的空隙可以容纳缩小版的上层，用图形表述如下：

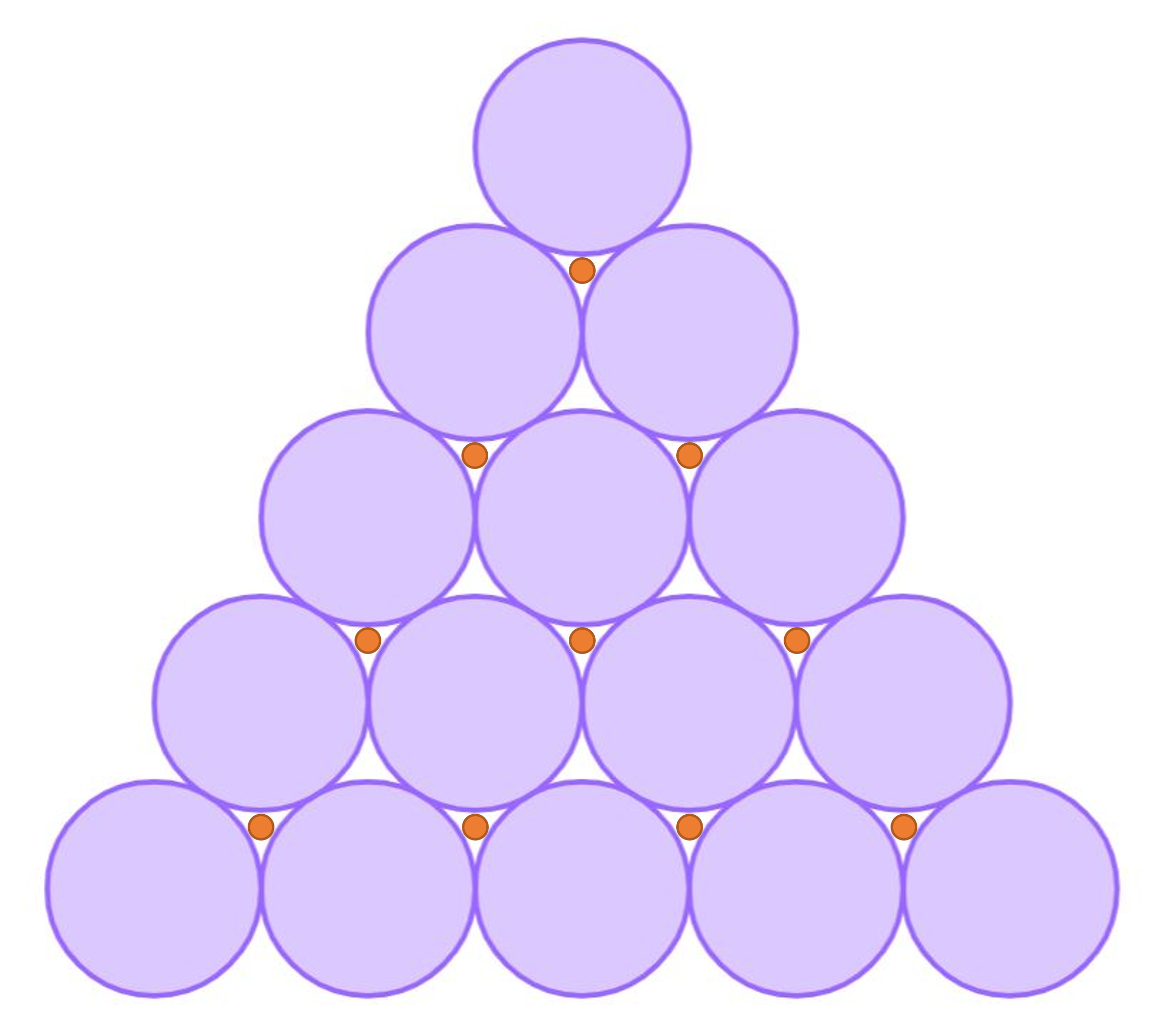
而且，对于立体最密堆积到四维空间堆积升维的过程，立体之外的那个维度上的层与层，投影回三维后，也有一种关系，即下层的空隙可以容纳缩小版的上层：

这似乎进一步印证了我们的猜想。

• 当 更大的时候还有三角撒星形垛，三角撒星更落一垛等等。

我们再介绍一种方垛，从最上层开始每层果子数为

有实物演示如下：

它对应的求和公式为：

朱世杰的著作中也有这一公式，此外，他还研究了更高次方的求和问题，可见他对垛积问题的研究是成体系的。可以用朱世杰恒等式对上式进行证明：

这种堆积形式还叫作体心立方密堆积，空间利用率为 ，铁、钠、钾等金属的晶胞是这种结构，在高中化学《物质的结构与性质》中曾介绍过。

从以上介绍可见，朱世杰是从农业生产生活中提炼出了堆垛求积这一数学问题，并给出了一个恒等式。这一问题对应着现代数学的高阶等差数列求和，又对应着组合数学的一些概念。我们不知道朱世杰当时是如何计算出的，但是我们可以用现代数学的方式给出证明：

根据最原始的公式

回归到单项式概念下， 代表着方程 的自然数解的个数， 代表着方程 的自然数解的个数，以此类推。根据上文的结论可以写出：

经过变量替换，得到：

得证。除此之外，朱世杰恒等式还有很多种证法，可以直接从其组合意义出发证明，也可以利用恒等式 证明，还可以用等比数列求和结合二项式定理证明。

稍微插入几句题外话，还可以发现 代表着 的自然数解的个数，意味着：

的自然数解的个数等于 的自然数解的个数。

单项式排序

通过以上讨论，我们知道了 的计算方法，那么我们用何种次序来书写这 个单项式呢？或者说 和 谁在前？

对 个单项式，我们有 种排序方式，其中有的排序是有规律可寻的，有的是毫无章法的，我们总不能每次都随心所欲地书写吧，有没有一种排序的准则呢？

有一种准则叫做 Graded Reverse Lexicographical Monomial Order，简称 GRevLex，翻译过来大概是『分级逆词序单项式排序』。规则如下：对于两个单项式 和 ，若 ，则前者的次序大（次序大意为排得靠前）。若 ，当向量 的最后一个非零元素为负，则前者的次序大。

举个例子，对于 和 ，或者叫做 和 ，因为二者次数相等，所以比较向量 的最后一个非零元素 ，由于 ，因此 的次序靠前。

直接通过 C++ 代码展示如何用 GRevLex 对这 个单项式进行排序：

nextOrder()函数输入一个 order，内部进行一些处理，把 order 变为下一个 order

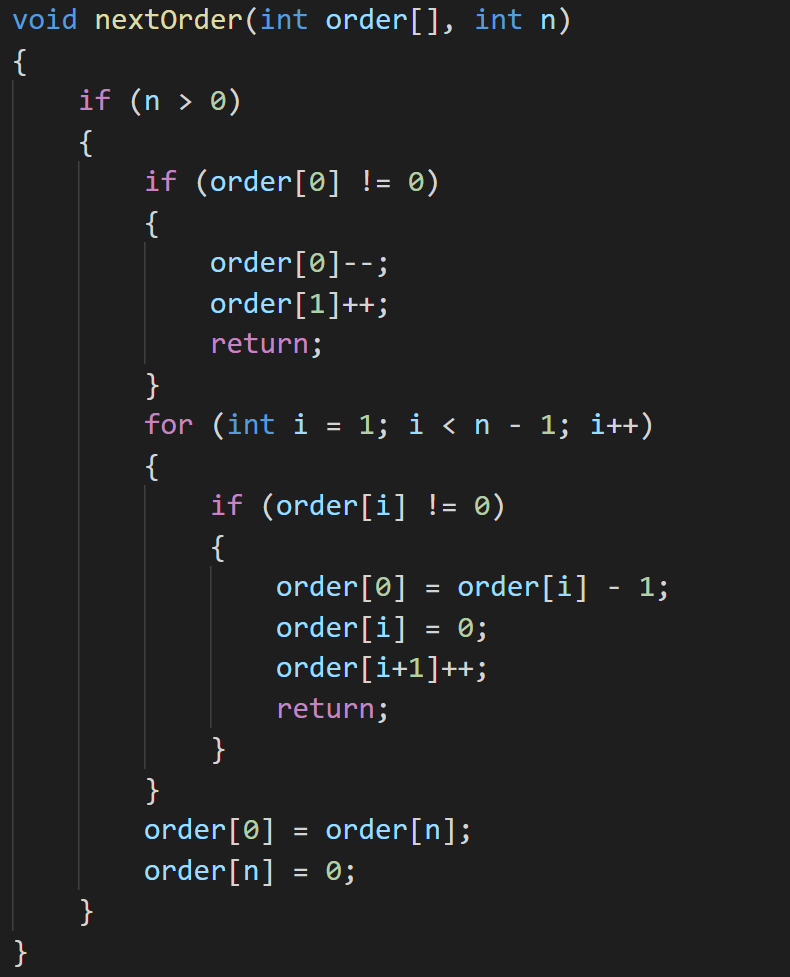
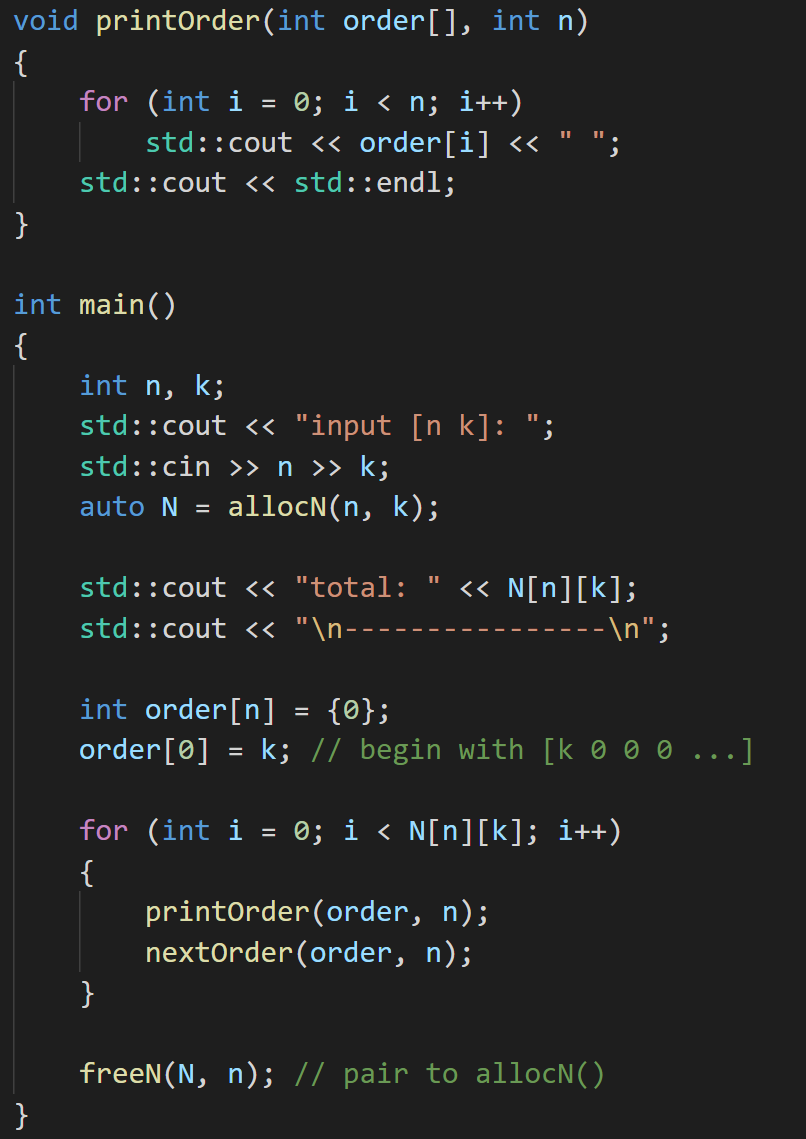
main()函数里，起始的 order 设为k 0 0 ...，然后对nextOrder()循环 次，并打印：

输入 ，，结果为：

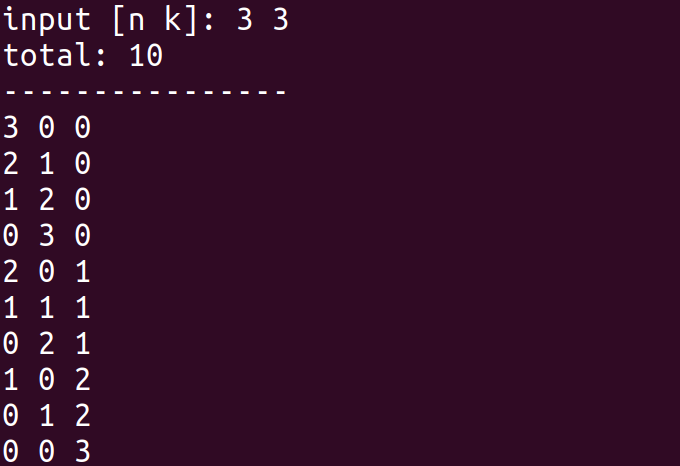
与之相应的排序为：

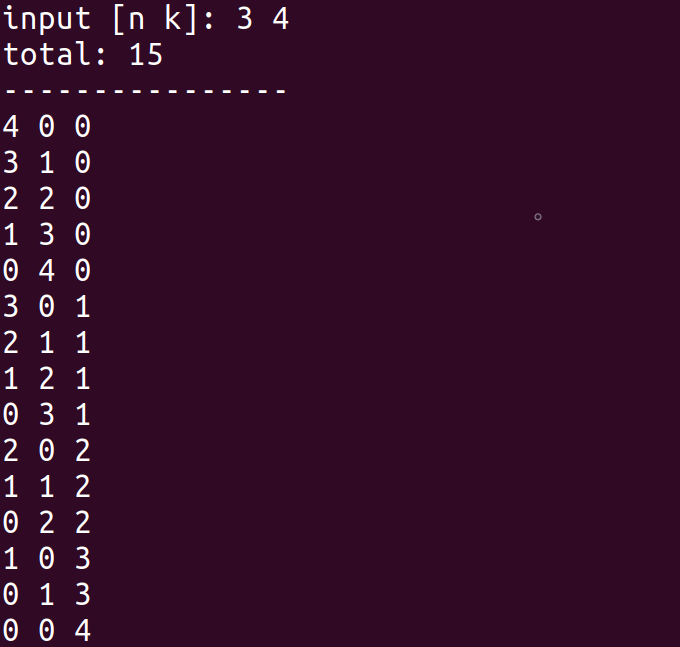
再比如 ，，结果为：