如何优雅地不定积分
2021-08-07 19:03:00
知乎上有一个不定积分王者 100 题集锦(直接搜索关键词就能找到),据答主自己说:
会做 3 道题,就足以应付相关考试
难道这就是传说中的:

那么,面对这 100 道难题,怎样才能显得从容不迫?莫非要靠手算?

看来手算显然不是。想要优雅地不定积分,不妨试试这三个工具:WolframAlpha、Integral Calculator和 Rubi 扩展包(其实主要想介绍 Rubi 扩展包,另外两个是拿来凑数的)
WolframAlpha
以一个简单的不定积分为例:
介绍 WolframAlpha 怎样优雅地完成不定积分(这个题比较简单,如果按照人的思维方式,肯定先尝试对
在 Mathematica 里连续按两次等于号,就会调出 WolframAlpha,输入表达式:
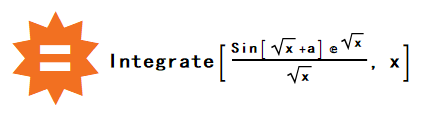
结果如下,WolframAlpha 给出了详细的积分步骤:

WolframAlpha 也是先对
除了在 Mathematica 里使用 WolframAlpha,还可以在网站 https://www.wolframalpha.com/ 或者移动端使用(网页版的 WolframAlpha 已经不能免费查看详细的积分步骤了,移动端目前还可以)
Integral Calculator
Integral Calculator 是一个免费的在线积分计算器,其主打的特点是可以给出详细的积分步骤。还有一个孪生的网站——导数计算器。
首先,输入被积表达式,一般的编程语言采用什么格式输入,这里就采用什么格式输入。输入的被积表达式会在输入框下方实时预览:

下面是官方给出的原理图,输入的表达式首先会采用调度场算法解析成机器容易理解的结构,然后用两种方式求解,一种用人类的思考方式进行求解,令一种采用 Maxima 进行求解。
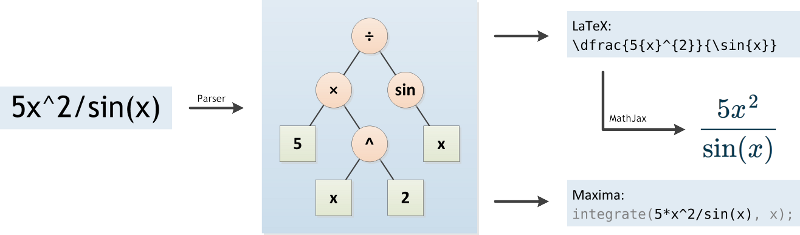
点击 Go! 按钮:

有些步骤会有( steps ),比如:
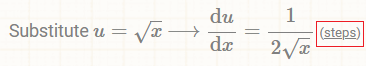
点击( steps )会跳转到孪生网站,进行详细的求导运算,甚至连求导公式的推导过程都会给出,非常适合自学:

然后,它还给出了另一种换元方法,点击下面的按钮:
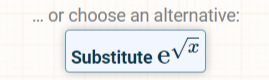
就会给出另一种换元的积分过程,结果如下:

Integral Calculator 和 WolframAlpha 的解法基本一致,Integral Calculator 还给出了另外一种换元方式
Integral Calculator 还可以指定上下界计算定积分:
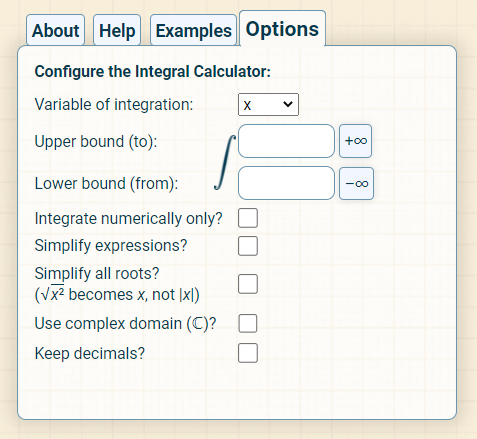
好家伙,要是把过程中的求导运算加上,这东西计算一次,比我当年的数学分析老师讲一学期的课讲得还多。

Rubi
前面介绍的 WolframAlpha 和 Integral Calculator,都是在线计算,虽然功能十分强大,但是计算的速度并不快,有时甚至需要等待十几秒,而且离线的时候根本无法使用。下面推荐的 Rubi 积分库可以做到离线快速不定积分,并且也可以给出积分步骤。
Rubi,Rule-based Integrator 的缩写,顾名思义,基于规则的积分器。官网给出的解释:一个基于大量积分规则系统的符号积分器:

官网地址是 https://rulebasedintegration.org/,开源地址是 https://github.com/RuleBasedIntegration/Rubi,Rubi 遵循的是较为宽松的 MIT 开源协议,意味着我们不仅可以任意使用、修改,甚至可以再发布:

安装与使用的教程可以在 Rubi 的官网查看。
安装
Mathematica 11.2 或更高的版本,直接运行下面的代码安装 Rubi:
PacletInstall["https://rulebasedintegration.org/Rubi-4.16.1.0.paclet"]
Mathematica 9 或更高的版本,先下载 .paclet 格式的扩展包,下载完成后,假设路径为 path,运行下面的代码安装 Rubi:
PacletInstall[FileNameJoin[{path, "Rubi-4.16.1.0.paclet"}]
卸载
Mathematica 9 或更高的版本,运行下面的代码卸载 Rubi:
PacletUninstall["Rubi"]
配置
安装完成后,需要运行:

或者

来加载 Rubi 扩展包。Rubi 的积分规则多达 6000 多条,初次加载大概需要 1-2 分钟的时间,因为初次加载会生成 .mx 文件,以后使用只需加载 .mx 文件,不到一秒就可以完成,可以用 RubiClearMemoryImages[ ] 函数清除 .mx 文件。
简单示例
使用 Mathematica 自带的函数 Integrate 进行积分:
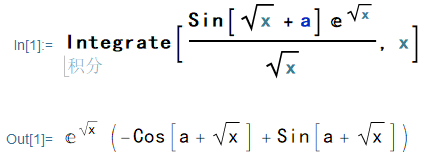
给出了正确结果,但是无法查看步骤。
下面使用 Rubi 提供的 Int 函数进行积分:
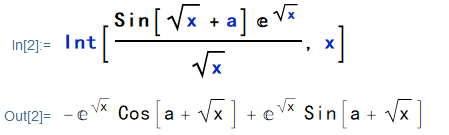
Rubi 也给出了正确结果,Rubi 最大的优点是可以给出积分步骤,使用 Rubi 提供的 Steps 函数查看步骤:
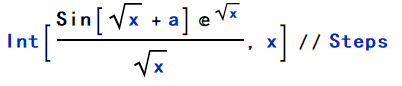
运行结果如下:

这乱七八糟的是什么鬼?

看似杂乱无章不知所云,其实只需牢记 Rubi 是基于规则进行积分的,就很好理解了,解释如下:
首先,Rubi 匹配出被积函数满足下面的形式:
而
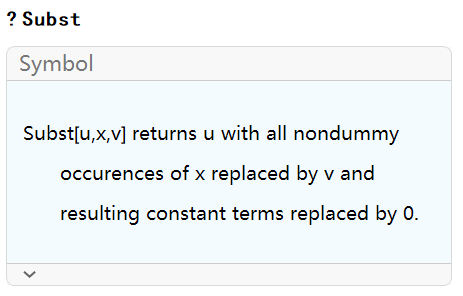
是可以进行换元的: Rubi 给出的结果里的 Subst 函数表示换元,可以查看该函数的说明:
换元之后,积分变成:
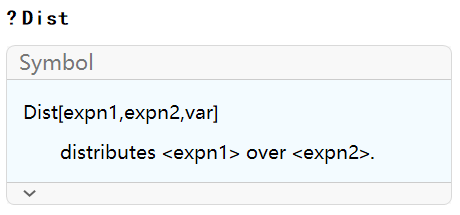
结果里的 Dist 函数表示提取,可以查看该函数的说明:
之后,Rubi 匹配到
满足下面的形式: 而
是可以直接写出原函数的。在原函数里代入系数 的具体值,并换元回来,就得到了最终的结果:
所以,Rubi 积分的本质就是对积分规则进行匹配,它不像在线积分那样灵活,甚至可以说只是在生搬硬套。不过基于庞大的积分规则库,Rubi 还是可以胜任许多的不定积分。
下面再看一个简单的例子:

用 Steps 函数查看步骤:
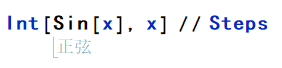
结果如下:

对于比较复杂的第一类椭圆积分,Mathematica 自带的函数 Integrate 可以识别出来:
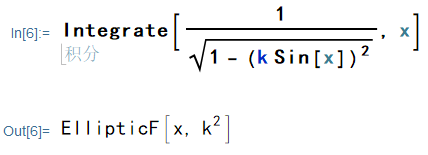
Rubi 也可以轻松匹配出:
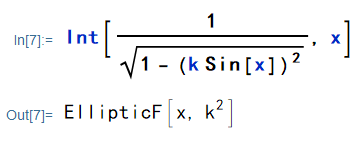
用 Steps 函数查看步骤:
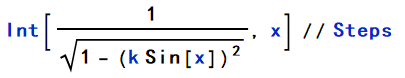
结果如下:

说明第一类椭圆积分也包含在 Rubi 的规则库里面。
Int 函数可以穿过列表 List,比如:
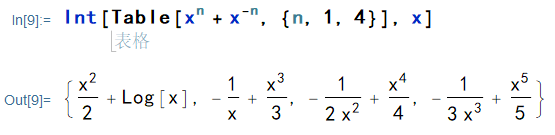
定积分
Rubi 也可以计算定积分,只需要在积分变量后指定上下界即可,比如:

通过查看 Rubi 的源代码,发现 Rubi 计算定积分的本质,是先计算不定积分,最后代入上下界,得到定积分。所以对 Rubi 来说,计算定积分和不定积分没有本质区别。

积分步骤输出成 LaTeX
Rubi 虽然能够给出积分步骤,但是步骤的可视化并不太直观,所以有大佬编写了 IntWithStepsOfTeXForm 函数,代码如下:
IntWithStepsOfTeXForm[formula_,j_]:=With[{TeX2Str=Convert`TeX`ExpressionToTeX},Steps[Int[formula,j],RubiPrintInformation->False]//Flatten//Most//Cases[RubiIntermediateResult[x_]:>"=&"<>(TeX2Str[HoldForm@@x])<>"\\\\"]//{"\\begin{aligned}",TeX2Str@HoldForm@Int[formula,j],Sequence@@#,"\\end{aligned}"}&//StringRiffle]
有了这个函数,就可以轻松地把积分过程输出成 LaTeX,下面进行测试:

配合 MaTeX 使用
上期已经介绍过 MaTeX 的使用方法,用 MaTeX 处理 IntWithStepsOfTeXForm 函数输出的 LaTeX 文本:
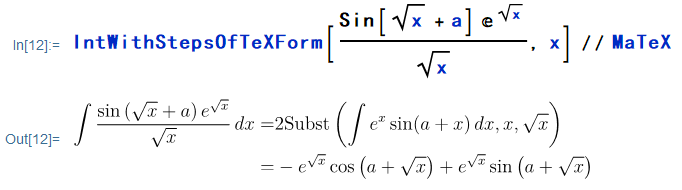
积分步骤的可视化已经非常明了了。
自定义积分规则
Rubi 的积分规则可以根据自己的需求进行扩展。查看 Rubi 的源代码,在 IntegrationRules 文件夹里存放的就是积分规则:
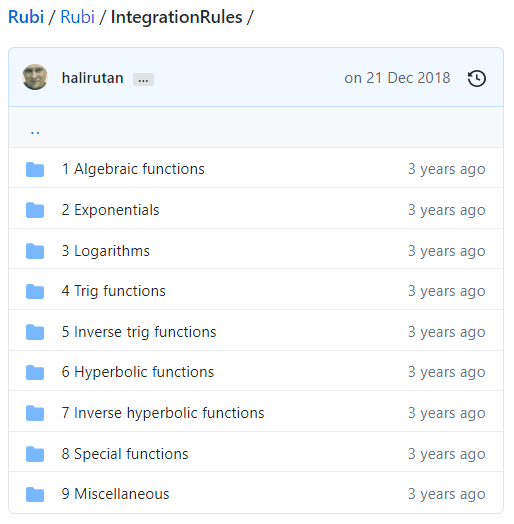
包括代数函数、指数函数、对数函数、三角函数、反三角函数、双曲函数、反双曲函数、特殊函数、其他函数等九大类。以
%5Em.png)
打开,查看源代码:
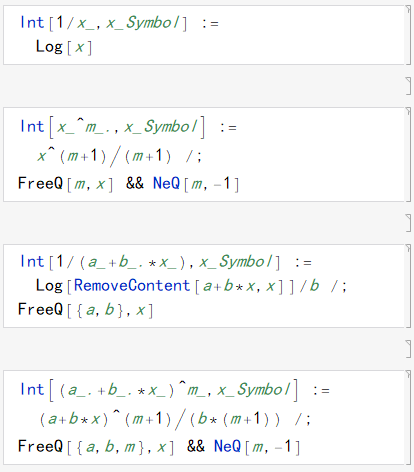
所以,按照这样的格式书写自己的规则,最后重新进行封装,即可。不过 Rubi 的积分规则已经很完善,一时很难找到需要补充什么,但是通过查看源代码,发现在加载规则时,特殊函数里的 Bessel 函数是被作者注释掉的,虽然不知道作者出于什么目的,但是可以用它来举例:
使用 Mathematica 自带的 Integrate 函数对第一类贝塞尔函数积分:

但是,因为 Rubi 没有加载 Bessel 函数,所以 Rubi 的 Int 函数无法匹配第一类贝塞尔函数:

Rubi 没能够计算下去。
使用下面的代码找到 Rubi 的安装路径:
PacletFind["Rubi"]
然后,打开 Rubi.m 文件,发现 Bessel 函数确实是被注释掉的:

把该行代码取消注释,保存文件,运行下面一行代码重新加载 Rubi,加载时间约为 2 分钟:
Get["Rubi`Rubi`"]
此时再次对第一类贝塞尔函数积分,就能计算下去了:

与 Integrate 函数只相差一个无关紧要的积分常数
测试
以知乎的不定积分王者 100 题中的一部分题目作为测试对象。

下面是 Rubi 的计算结果:

结尾
本文介绍了 WolframAlpha、Integral Calculator和 Rubi 扩展包三个积分工具,下面对三者进行对比:
| 在线 | 速度 | 机制 | 分部积分 | 步骤 | 可视化 | 费用 | |
|---|---|---|---|---|---|---|---|
| WolframAlpha | 是 | 慢 | 不清楚 | 可以 | 详细 | 明了 | 收费 |
| Integral Calculator | 是 | 慢 | 模拟人类、Maxima | 可以 | 很详细 | 明了 | 免费 |
| Rubi | 否 | 快 | 匹配规则 | 不可以 | 简略 | 一般 | 开源可扩展 |