其实本文的所有代码，早在 1 月份寒假的时候就写好了，趁着公众号刚刚创号，发出来助助兴。

本文受视频《Times Tables, Mandelbrot and the Heart of Mathematics》的启发。

心形线与模乘运算

先做一个实验，把圆周等分成 10 份，等分点依次记为 ，效果见下图：

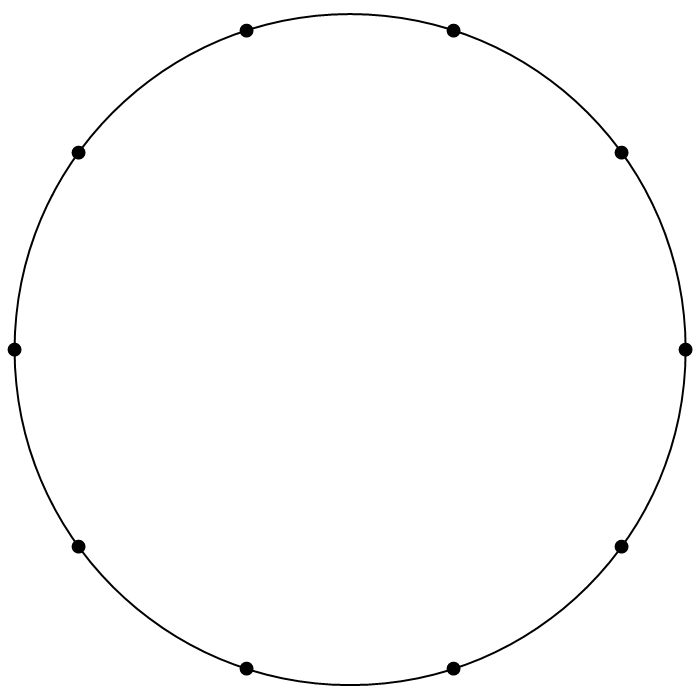
Mathematica代码如下

可以复制的文字版本

Show[Graphics[{FaceForm[], EdgeForm[Black], Disk[{0, 0}, 1]}], Graphics[{PointSize[Large], Point[CirclePoints[{1, 0}, 10]]}]]

对于 ，把圆周上的第 个等分点和第 个等分点相连，其中表示模乘运算。另外，如果 ，则把第 个等分点和第 个等分点相连（因为我们并没有定义第 个等分点，所以认为第 个等分点就是第 个等分点），简单来说，就是下面的连接方案：

注意到 时， 自身连接是没有意义的，所以忽略掉了。连接的结果是下图的样子：

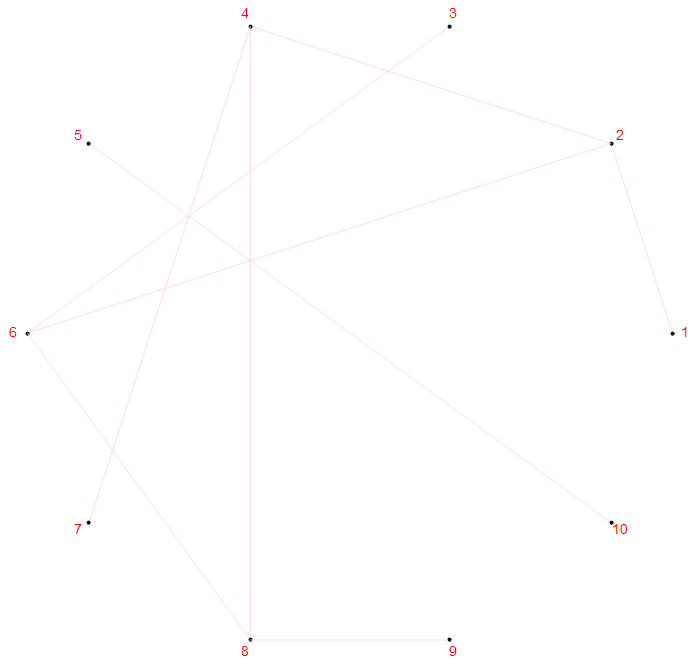
的确，看不出任何规律。如果把 增加到 呢？对于 ，把圆周上的第 个等分点和第 个等分点相连，变成了下图的样子：

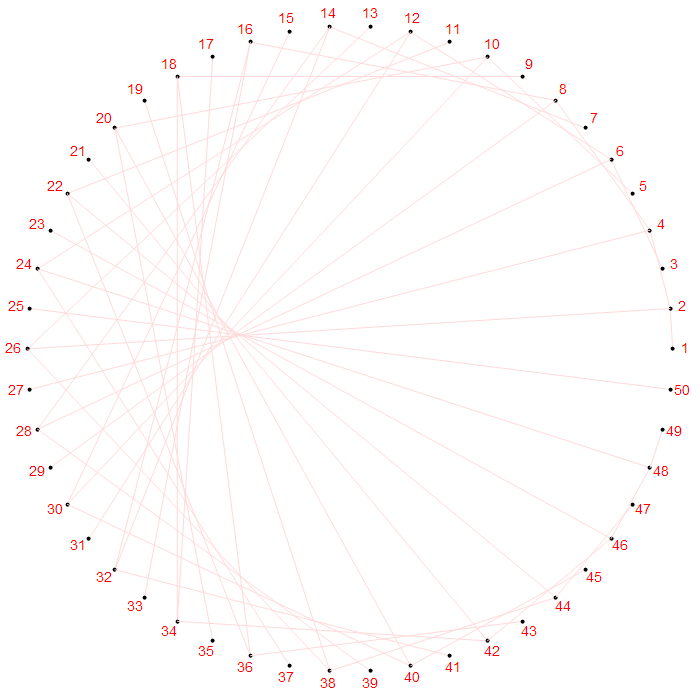
隐隐约约能看出点东西了。再把 增加到 呢？见下图：

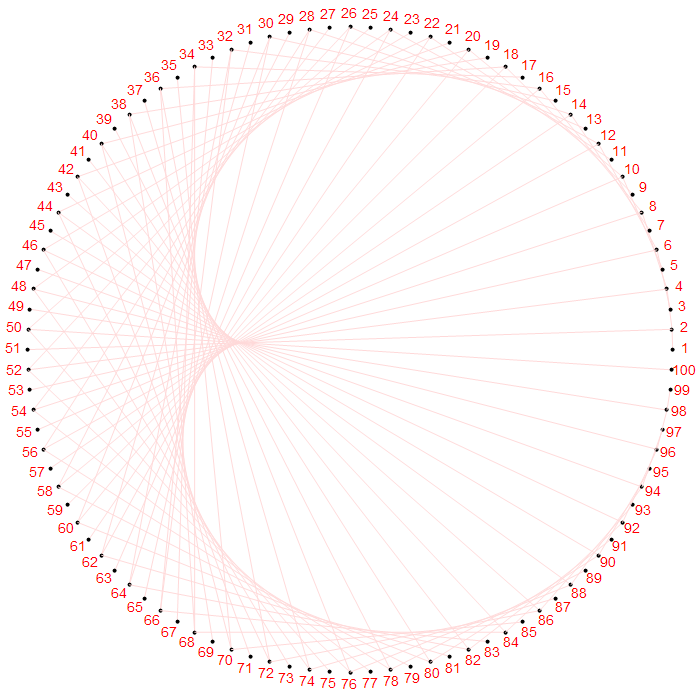
这不是笛卡尔的心形线吗。让我们把从 到 的全过程展示出来：

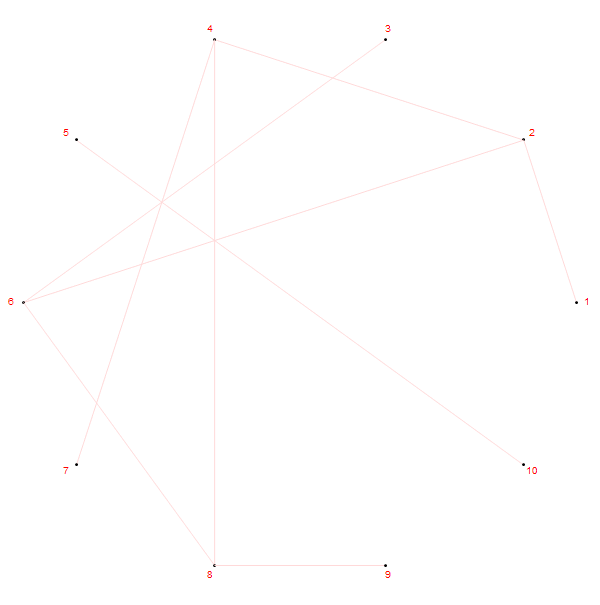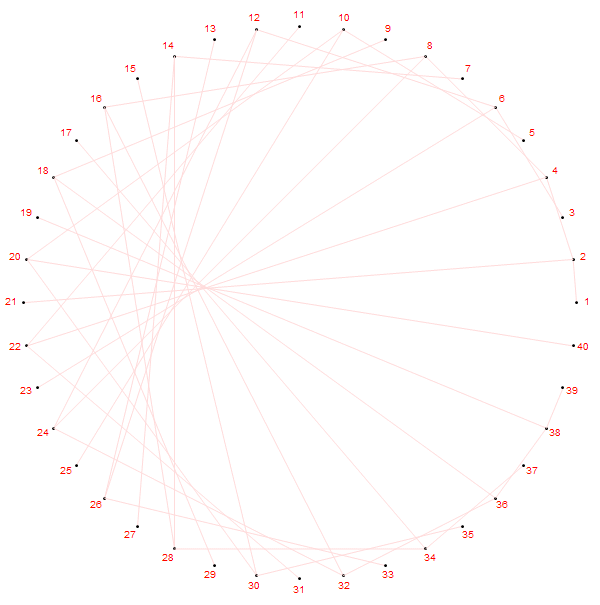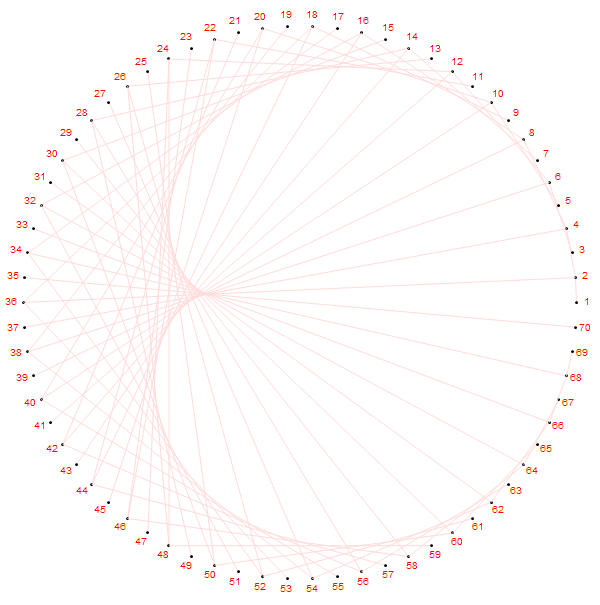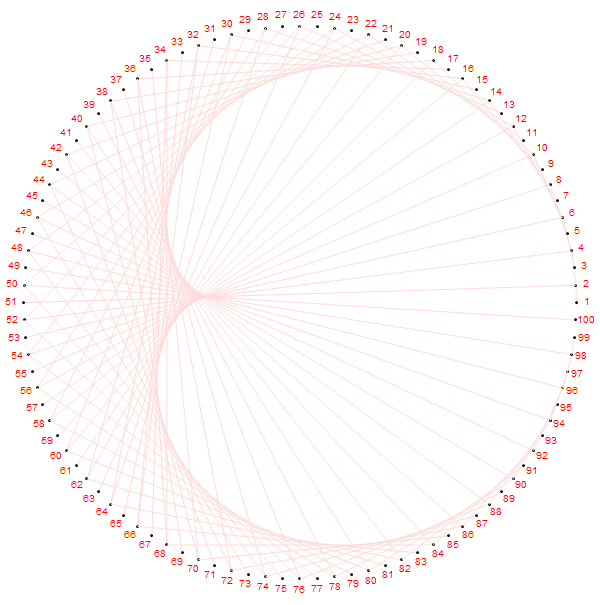
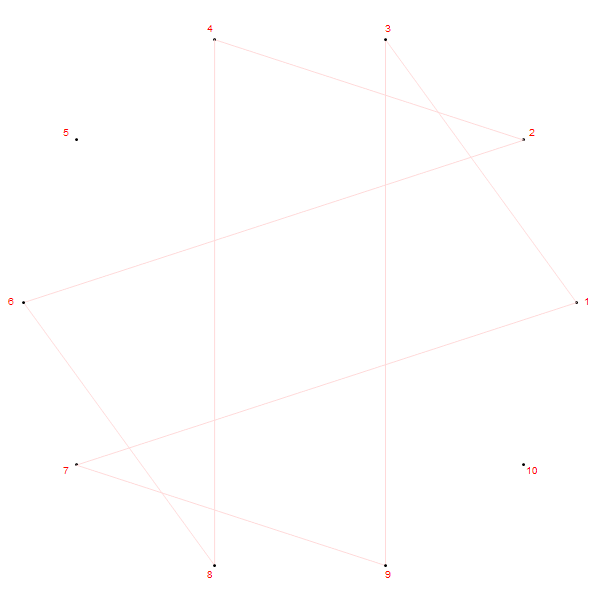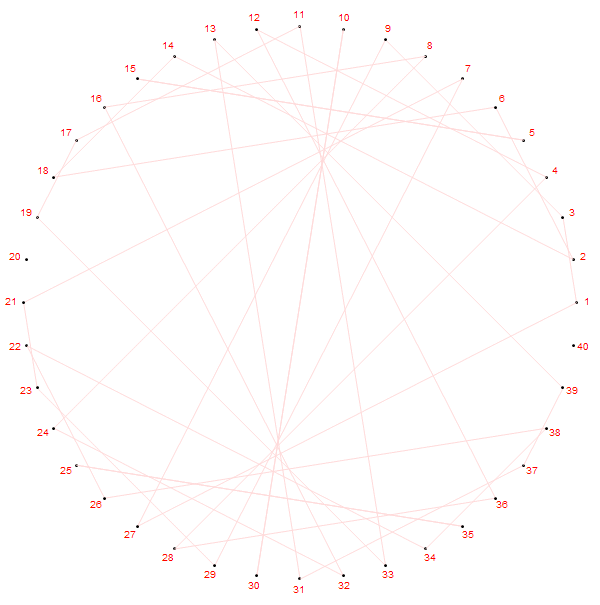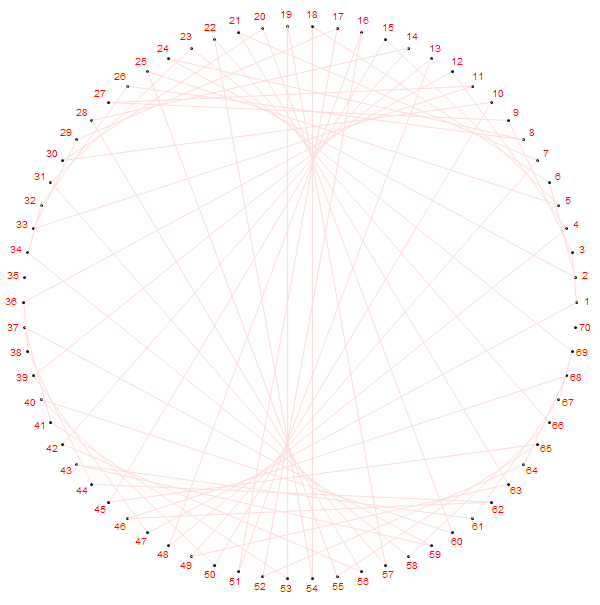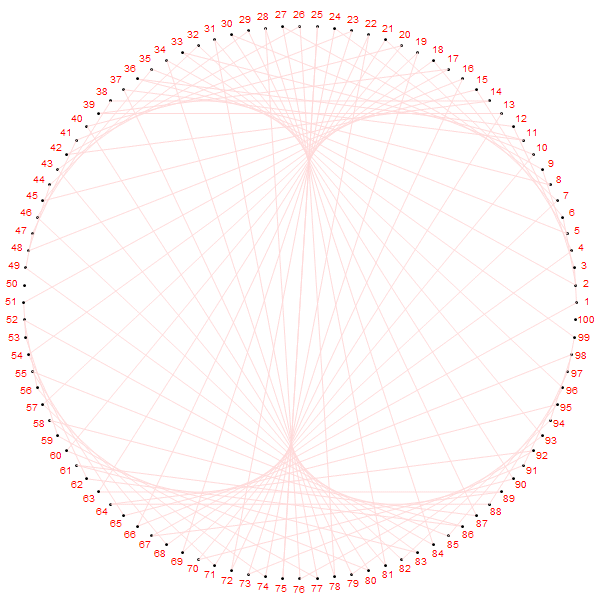
如果稍微更改规则，把圆周上的第 个等分点和第 个等分点相连，又会变成什么样子呢？话休饶舌，直接上动图：

第 个等分点和第 个等分点相连：

第 个等分点和第 个等分点相连：

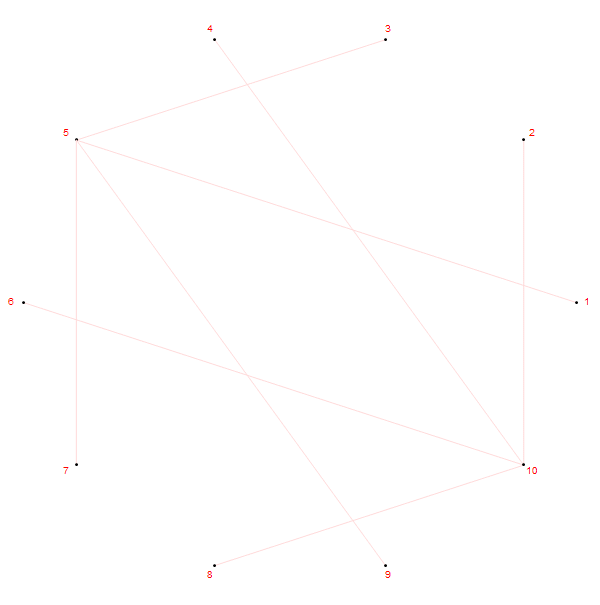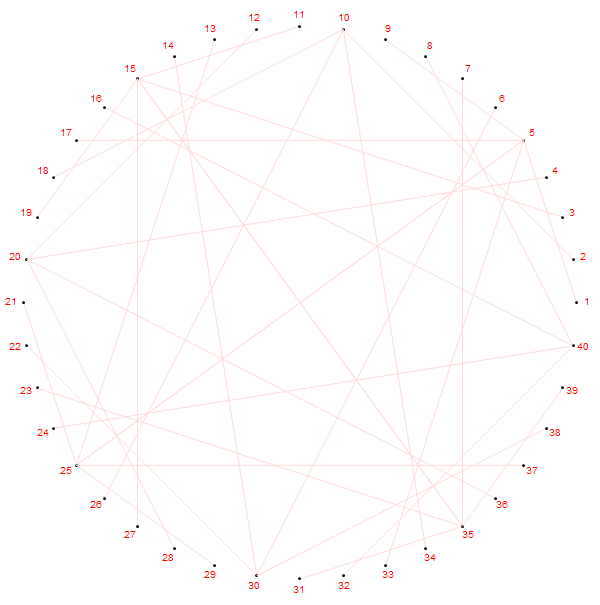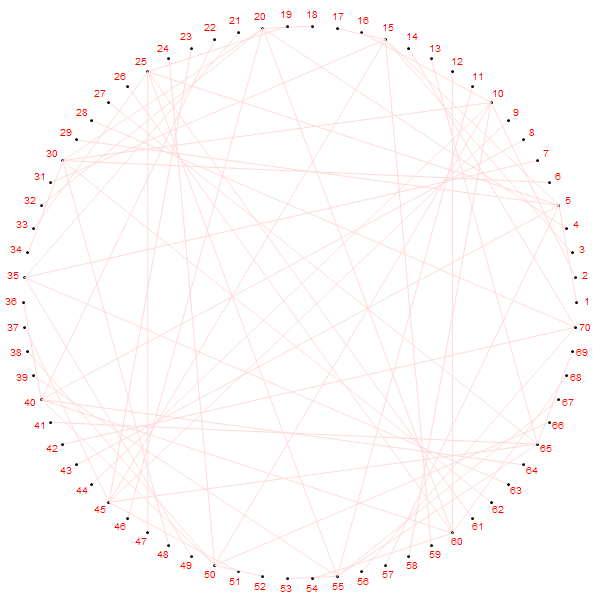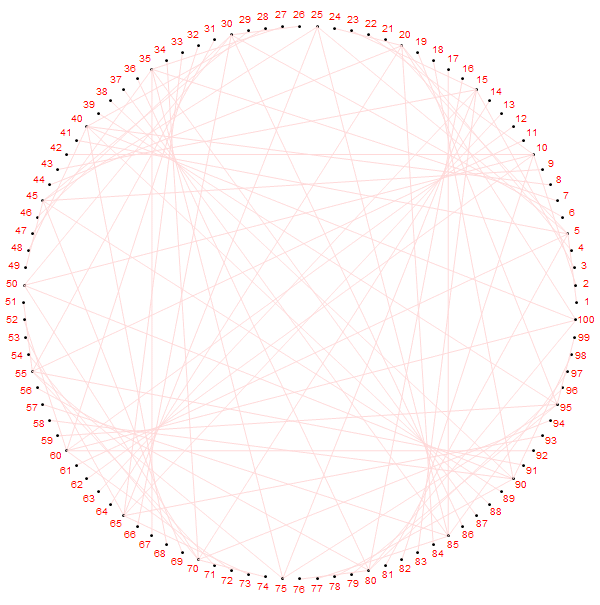
嗯，有点意思。以上的所有图片都是用Mathematica生成的，代码只有两行.........(MATLAB 出来挨打)

可以复制的文字版本

Heart[n_, m_] := (H = CirclePoints[{1, 0}, n]; Graphics[Join[{{LightRed, Line[{H[[#]], H[[Mod[m*#, n] /. {0 -> n}]]}]}, Text[Style[#, Red], 1.04*H[[#]]], Point[{H[[#]]}]} & /@ Range[n]], ImageSize -> 500]);
Manipulate[Heart[n, m], {{n, 100, "等分份数n"}, 10, 100, 1}, {{m, 2, "模m"}, 2, 5, 1}]

而且可以直接交互式操作.........(MATLAB 已经哭晕在厕所)

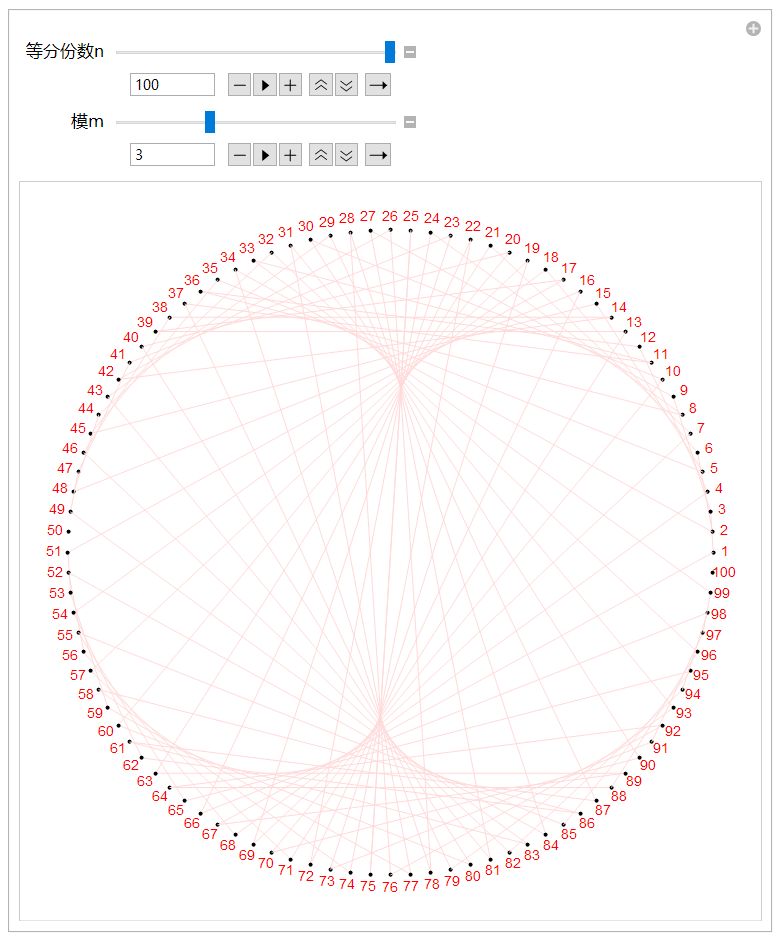
心形线

众所周知，心形线是一个圆在另一个圆的外侧无滑动滚动产生的，上动图上代码.........(MATLAB 你坐下)

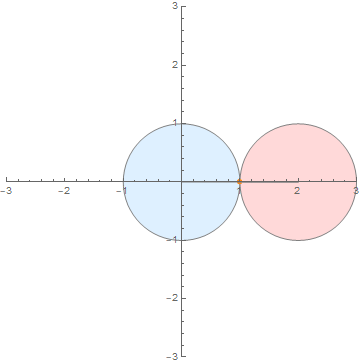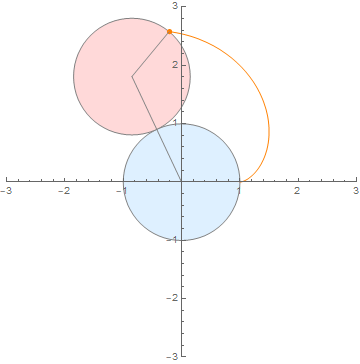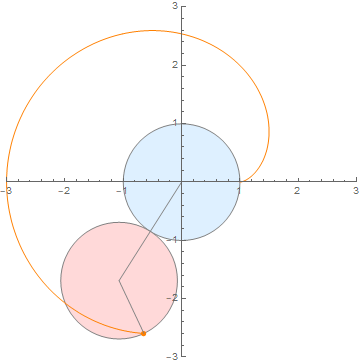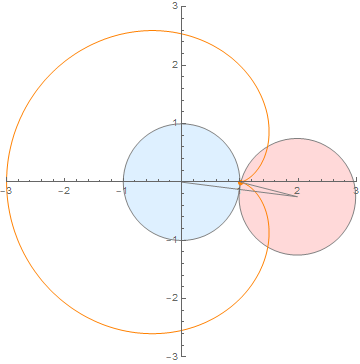
（内外两圆半径之比为 1:1）

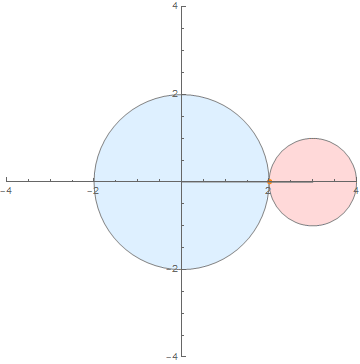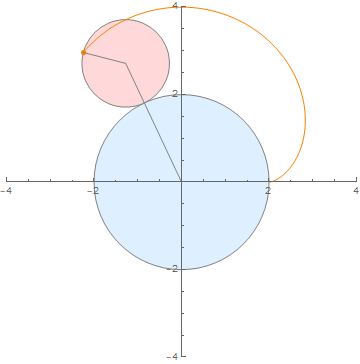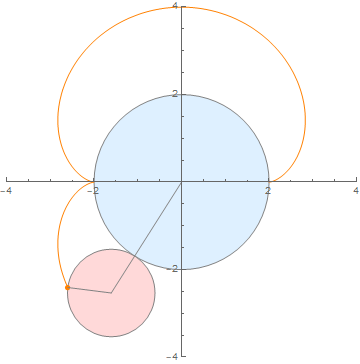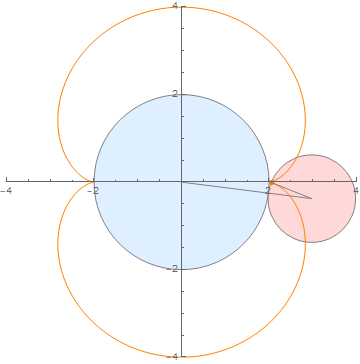
（内外两圆半径之比为 2:1）

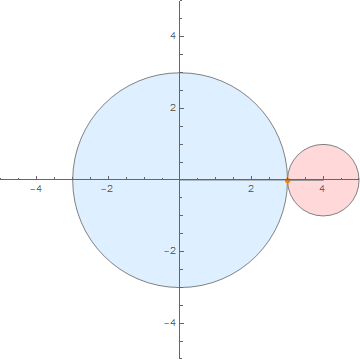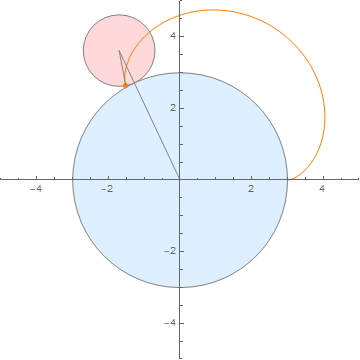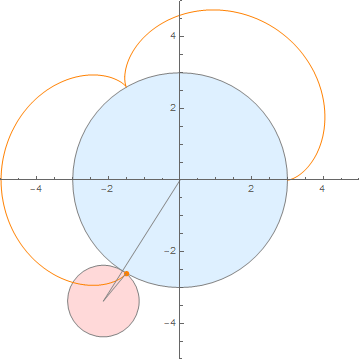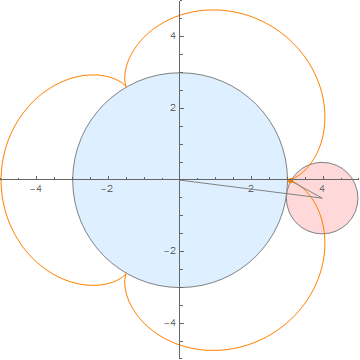
（内外两圆半径之比为 3:1）

Mathematica代码如下（其实只有三行）

解释一下，其实很简单，只需要直角坐标的参数方程。假设内圆半径为 ，外圆半径为 ，则参数方程为

曼德勃罗集

在复数域，令迭代公式为 ，其中 ，固定 ， 的取值遍历整个复平面，迭代一定的次数后，使得迭代过程收敛的 构成的集合，称为曼德勃罗集，收敛指标一般取 。（大多数情况，只关心 这一正方形区域，而并非整个复平面）

先从解析法的角度分析这一过程：

① 迭代 1 次时，满足收敛指标的区域为

从解析式可以看出，是圆形，长下图的样子：

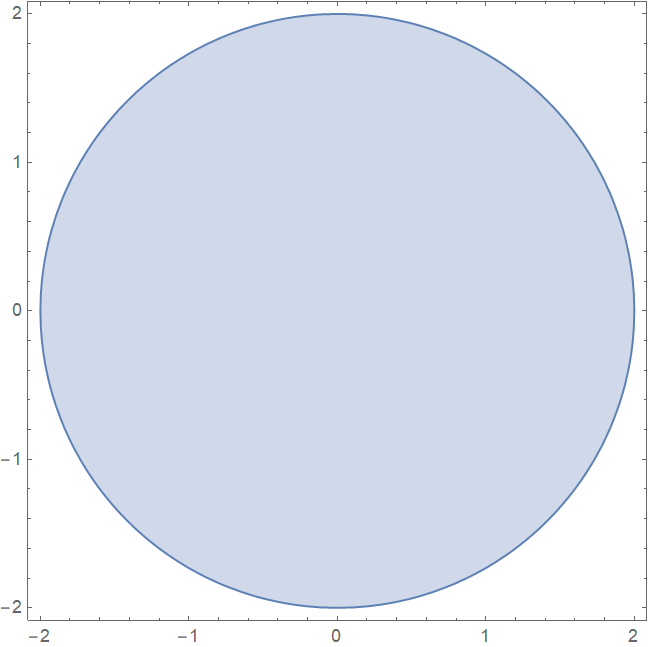
② 迭代 2 次时，满足收敛指标的区域为

有点像椭圆：

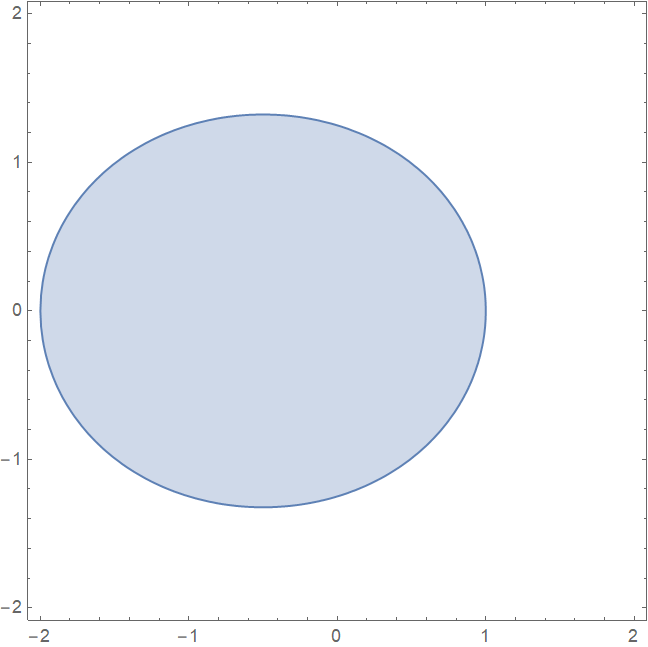
③ 迭代 3 次时，满足收敛指标的区域为

像是自行车的座椅：

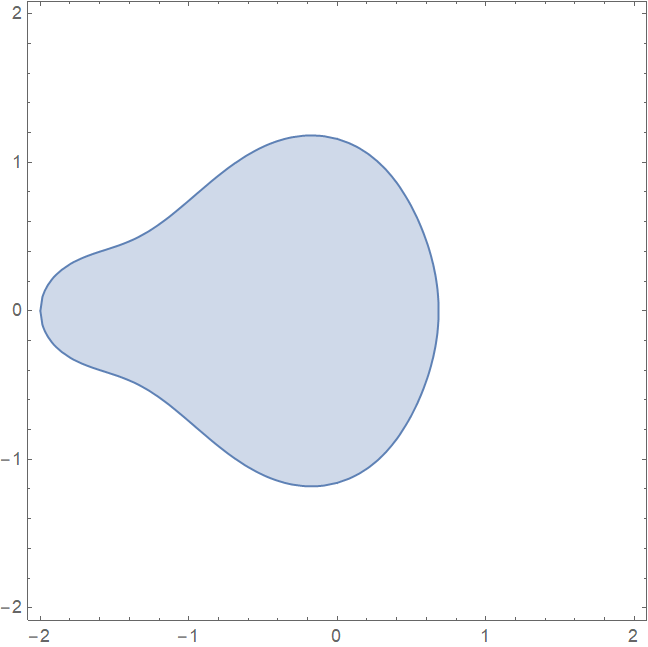
可以预见到，如此迭代下去，收敛区域 的解析式将变得极为复杂，在Mathematica里对该解析式进行化简，程序如下

备注：这个代码是有技巧的，必须一边迭代一边展开，最后一步需要对 Re[z]^2+Im[z]^2 进行幂展开，而不是对 Abs[z]^2 进行普通展开，并需要指定 和 属于实数域，否则得不到想要的结果。

代码执行的结果为：

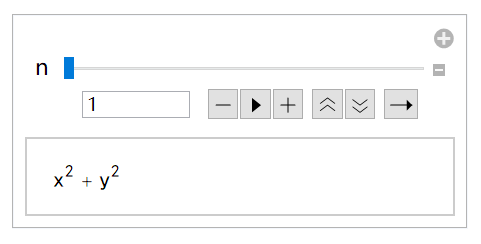
（迭代次数 n=1，形式很简单）

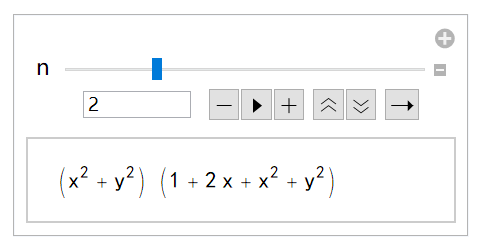
（迭代次数 n=2，形式并不复杂）

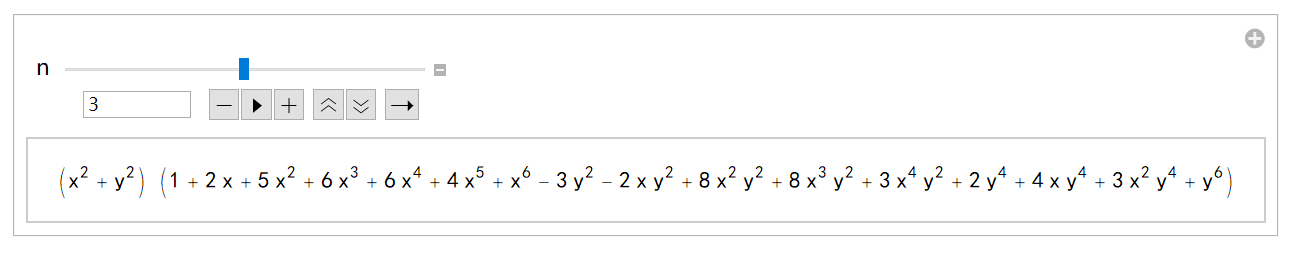
（迭代次数 n=3，战场态势瞬息万变）

（迭代次数 n=4，场面逐渐失控）

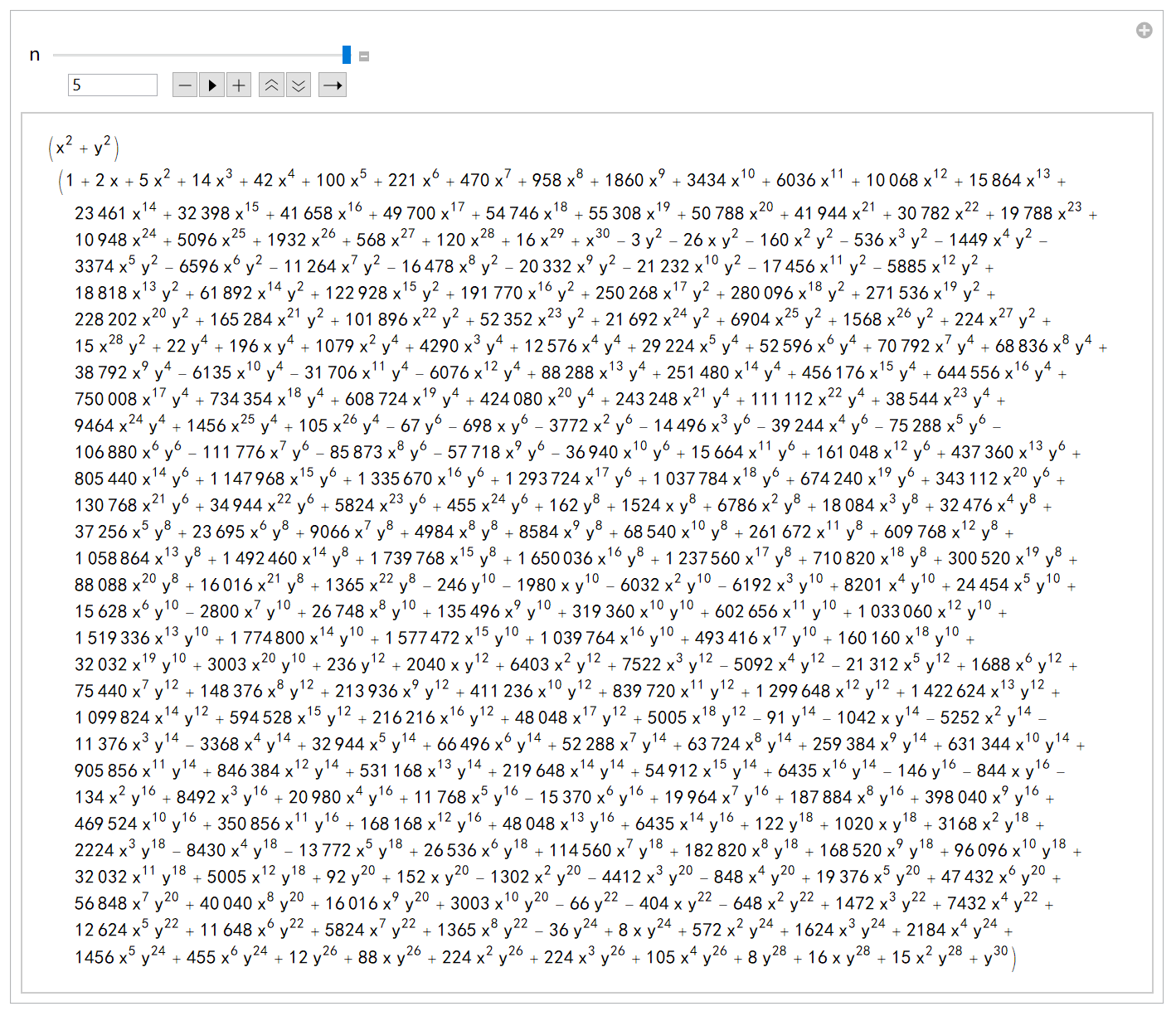
（迭代次数 n=5，场面已经失控）

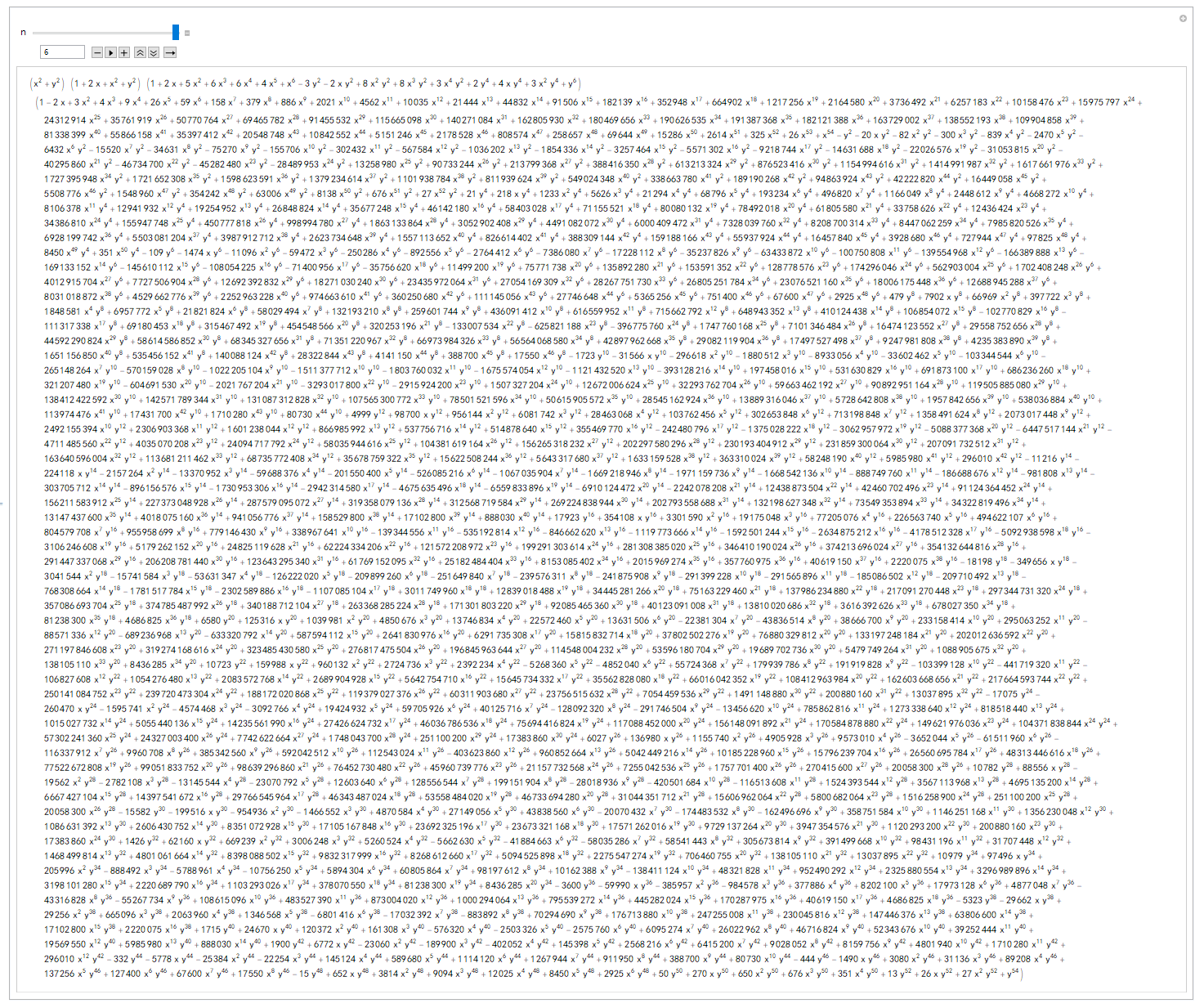
（迭代次数 n=6，场面彻底失控）

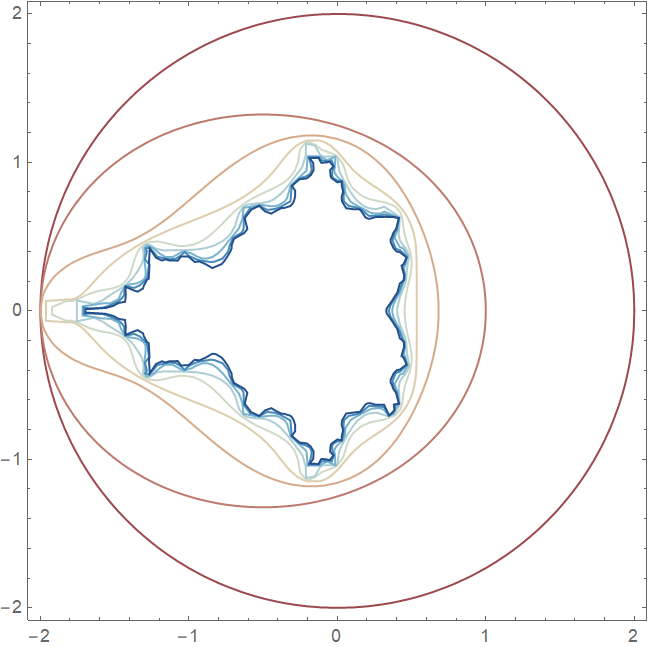
上面的一系列表达式其实就是曼德勃罗集合的边界。随着迭代次数的增加，集合的边界会变得极为复杂，最终的归宿将是处处连续、但处处不可导，也就是大名鼎鼎的曼德勃罗分形。在Mathematica里计算出迭代次数从 1 到 9 的收敛区域表达式，并作出表达式对应的边界形状，程序如下

边界的形状：

以上从解析法的角度进行了分析，但实际上数值法更有使用价值，当迭代次数增加到几十次、上百次时，解析法并不是一个好的选择。下面是用数值法生成的图形：

最后，不妨稍微更改一下迭代规则，把次数改为 3 ，对应的迭代公式变成 ，新的图形为：

心形线与曼德勃罗集

把上文提到的几类图形放在一起进行对比，似乎带有某种规律：

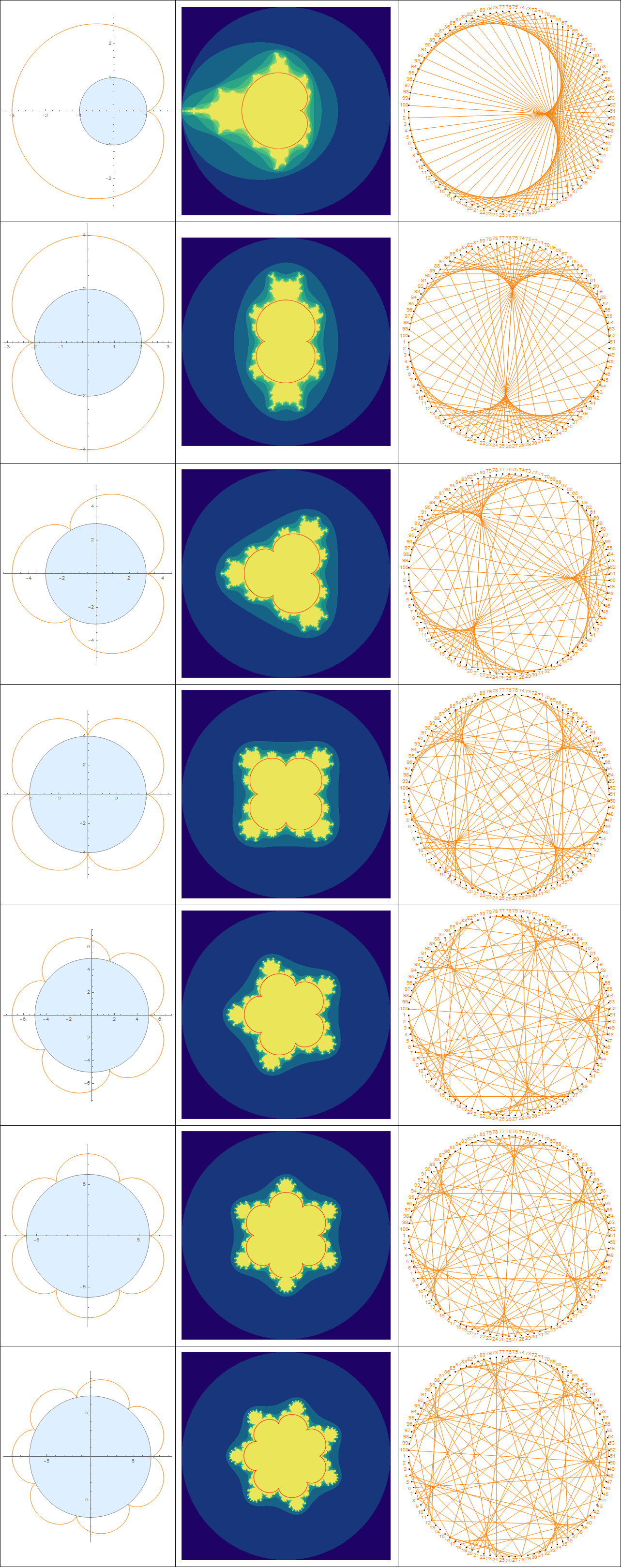
代码如下

参数方程、复数域的迭代函数、模乘运算，看似毫无关系的三个名词，却在这里体现出了数字的秩序。

结尾

一个有趣的实验（视频来源于知乎）