最小二乘解与最小范数解
2023-11-29 14:00:00
线性方程组
Least-Square
Least-Norm
这次我们就来厘清二者的区别。
超定方程组与欠定方程组
超定(Overdetermined)指的是方程组(约束)的个数多于变量的个数,即
欠定(Underdetermined)指的是方程组(约束)的个数少于变量的个数,即
最小二乘解
由于
并寻找
求解
由于
,寻找 最小即寻找 最小,而 它关于
的梯度为: 于是:
假设
可逆,则:
几何解释
由于
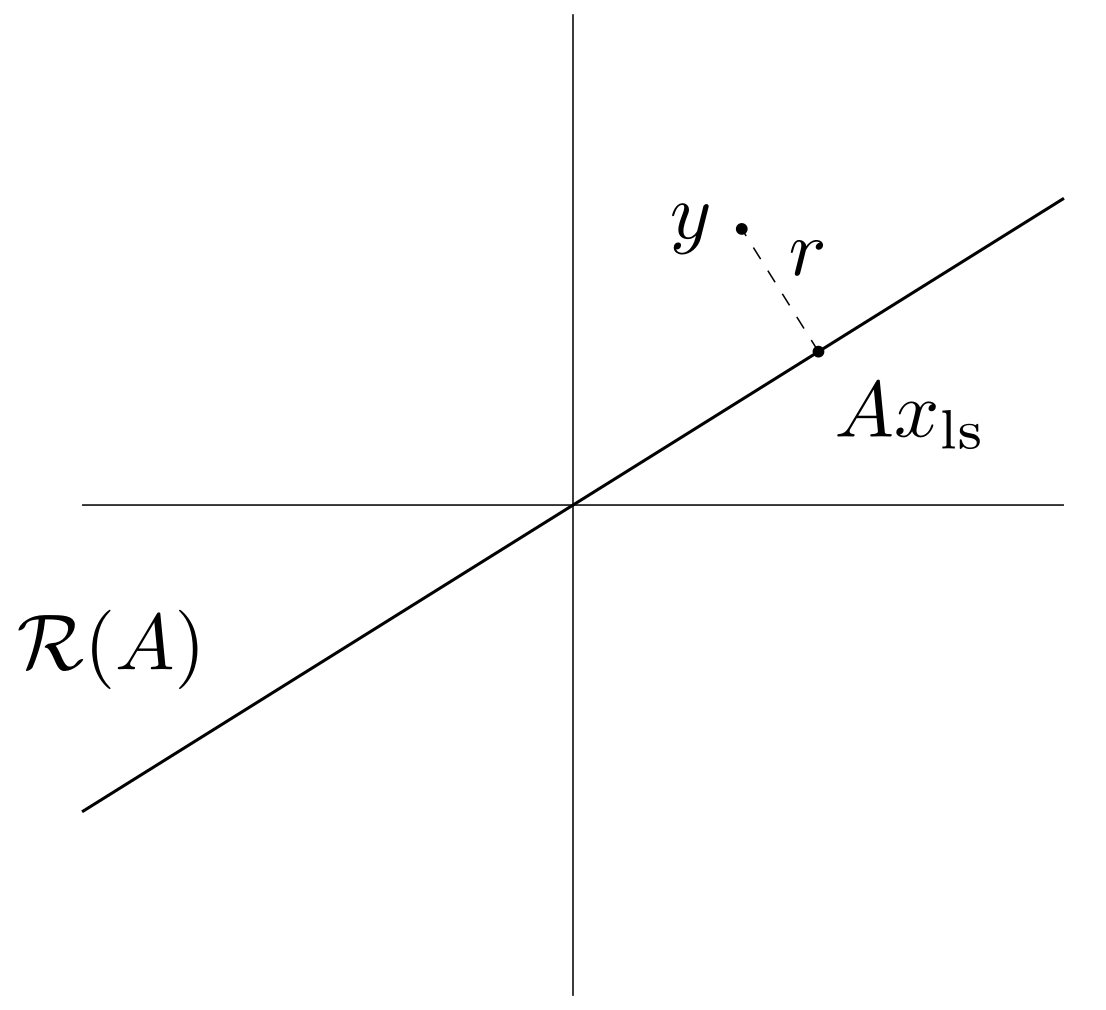
最小范数解
我们从欠定方程组的众多解当中挑选出范数最小的那个,用最优化的语言描述就是:
求解
用拉格朗日乘子法进行求解:
构造:
最优化的条件为:
于是:
几何解释
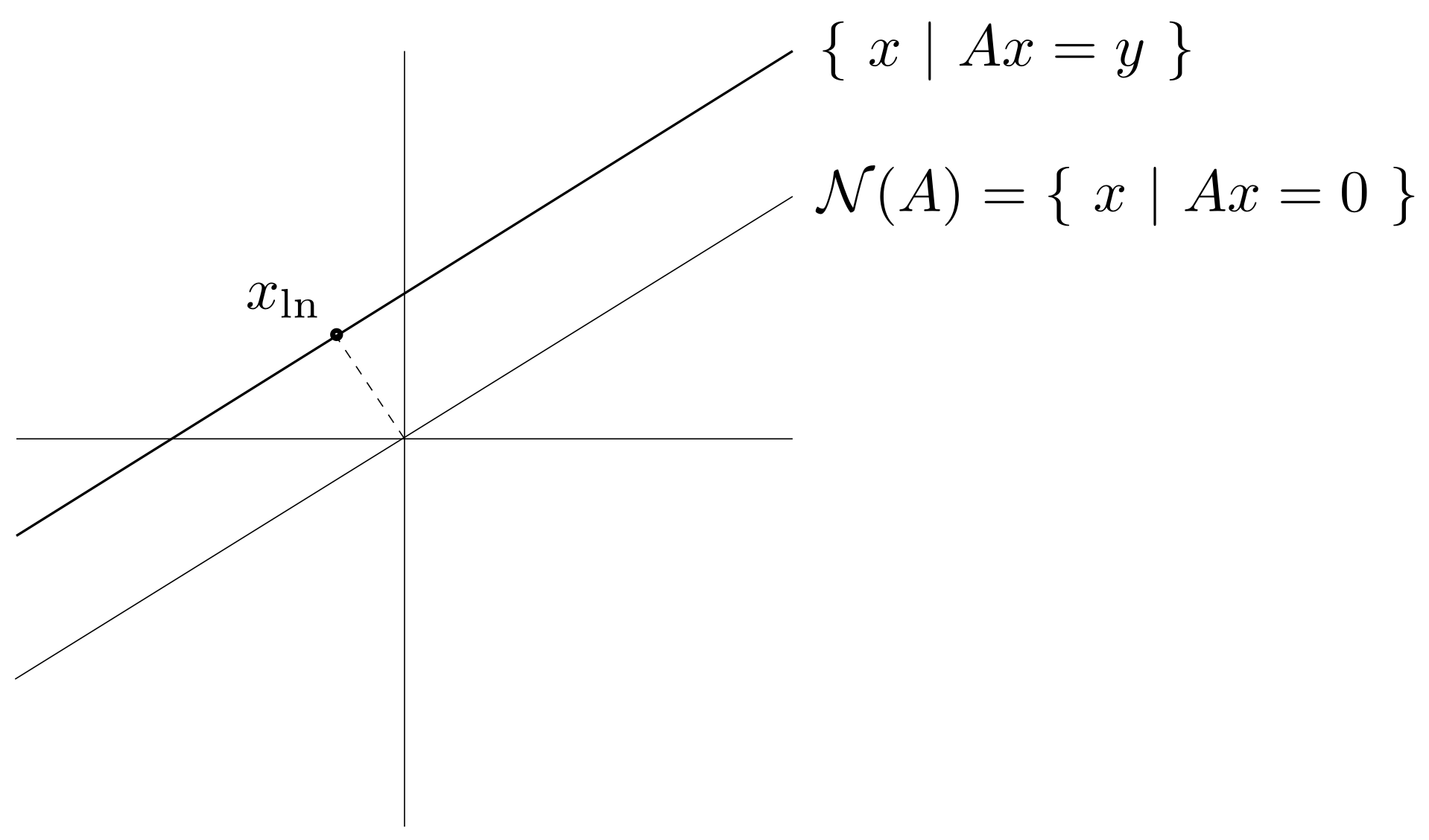
最小二乘解与最小范数解