势能多出一个常数项

根据初等轨道力学的知识，航天器在中心天体引力场的势能是：

当然，这是把无穷远当作零势能点。

由于势能是标量，那么航天器在两个天体引力作用下的势能就是标量的叠加，即：

但是，在 Wang Sang Koon 等人编写的专著《Dynamical Systems, the Three-Body Problem and Space Mission Design》的公式 (2.3.4)，把引力势能写成了：

怪就怪在它相比传统意义来说多出一个常数项：

Wang Sang Koon 等人紧接着解释道这是约定俗成的，且不会对运动方程产生影响。此外便没有更多解释，原文如下：

The constant last term in the expression for is added by convention (see, e.g., Llibre, Martinez, and Simo [1985]), and will not affect the equations of motion.

诚然，高中生都知道势能的大小与基准（零势能点）的选取有关，多出一个常数项仅仅意味着零势能点的变动，而不会对运动造成任何影响。就像我可以说我 1 岁，因为我把基准设为 2020 年，而不是 2000 年，我本身不会因此受到影响。

问题就在于，为什么要把势能表达式变得更加复杂？而且约定俗成说明大家都接受了这种做法，比如刘林等人的专著，以及绝大部分的论文都是这样的，究竟为什么？

Wang Sang Koon 让我们另请参阅 Llibre 等人的论文，我以为这么做的第一人就是 Llibre，能从中找到根源，然而并没有，他们也是沿用的这种写法。

广义能量

沿用多出一个常数项的写法，把势能写成旋转坐标系位置分量的函数：

虽然字面上和数值上都没有变化，但应该认清这里 和 都是旋转坐标系意义下的。而且限制性三体问题有：

经过一些不太讨人喜欢的坐标变换，可以得到动能的表达式：

那么，Lagrange 函数为：

根据 Euler-Lagrange 方程：

得到

再经过一些不太讨人喜欢的化简，我们有

这里引入一个新的记号 ，它被称作增强势能或有效势能：

此时，Hamilton 量，或者叫做广义能量，就是

非常微妙的形式，不展开。

观察到：

即

一般称 为 Jacobi 常数或 Jacobi 积分，它是限制性三体问题的第十个积分常数，此外再找不到第十一个。而且可以发现 ，所以它在一定程度上能反映能量水平，因此也有人称其能量或能量积分。

我的一些猜测

因为

则

对于平动点来说

因此，平动点的广义能量

进而

到此终于能进入正题了，对于三角平动点，有 ，此时 。

试想，如果在推导之初，不给势能多加一个常数项，此时三角平动点的广义能量就是：

它将随着系统参数 的变化而变化，也就是说不同系统有不同的三角平动点广义能量，这会使得结果不太优雅。

而且后面将介绍三角平动点广义能量是一个很有代表性的特征参数，它是 5 个平动点的广义能量的最大值，给势能加了一项后，这个参数永远是 ，这会很方便分析问题。

现在，即使你不了解 Hill 域也没事，只需知道下面 5 种情况：


, , 是共线平动点的广义能量， 是三角平动点的广义能量。随着参数 的变化，有一张很常见的曲线：

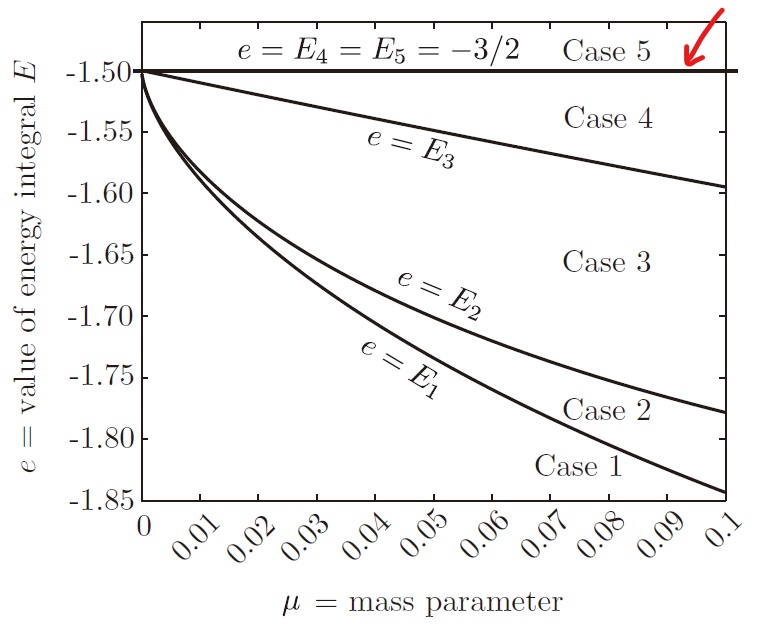
Case 5 与 Case 4 的分界线是一条直线！！！它的值就是三角平动点广义能量 。

当然了，这是由势能多出常数项出发，进而导出的一个现象。虽然它巧合得不像是巧合，我们却不好从结果来断定原因，并不能据此断定当年人们就是为此才约定给势能后缀一项，但是这必定是这一约定的一个意义所在，我总算能心安理得地接受这一定义。至于何人在何处率先使用这一定义，其出发点究竟为何，我读的文献尚且很少，至今还没有考证出来【笑cry】。