一元幂级数有着非常简单的形式：

它非常易于编程实现，即便是两个幂级数相乘，也只是 C 语言练习题的难度水平。但是，多元幂级数的编程实现难度如何呢？以三元幂级数为例，写出它的具体形式：

仅仅写到三次项，就令人眼前一黑。随着阶次的增加，会越发难以书写和表达。这种难以表达，不仅是对于人类而言，对机器也是。如果计算两个多元幂级数相乘，更会是一团糟。

齐次多项式

先明确一些概念：

单项式，指的是由数字或字母的积组成的代数式，记为 ，省略了系数，其中 为变量， 为常量。

多项式，即若干个单项式相加组成的代数式。

齐次多项式，即组成多项式的若干单项式具有相同的次数。变量数为 、次数为 的记作 。

上述多元幂级数其实可以拆分为多个齐次多项式的和，即 ，所以研究多元幂级数的前提是研究齐次多项式 。

我们之前探讨过变量数为 、次数为 的单项式的种类数 ，并且用 Graded Reverse Lexicographical Monomial Order (GRevLex) 对其进行了排序。这些 个单项式的和便是变量数为 、次数为 的齐次多项式。

需要明确一点，齐次多项式里各单项式的排序是确定的，即 GRevLex，那么只要掌握了带有次序的单项式的系数，就在实质上掌握了这个齐次多项式。我们对齐次多项式的所有操作，包括数乘、乘法、幂运算等等，实质都是在操作系数。为了存储各系数，比较简单的做法是直接动态分配 大小的double类型数组，这样我们就把齐次多项式抽象成了内存里的一维数组，这是最简单也是最自然的逻辑。但是问题在于难以索引，比如索引 对应的系数，我们需要先要执行一遍 GRevLex，获得 对应的序号，然后根据序号取数组里存储的系数。对于需要频繁的索引系数的场景，每次都要走一遍 GRevLex 的流程，这样的开销会显得我们很呆，是难以接受的，我们必须做出一些优化。

多叉树

树结构可以实现方便快捷地查找。为了利用这一特性，我们需要花费一番心思把齐次多项式改造成树结构。对于 ，当 且 时，把向量 的最后一个元素 分离出来，得到新的向量 。用 构造齐次多项式 ，则：

逐代分解下去，直到 或 为止，得到的便是树状结构。

时，齐次多项式退化为单项式，没法也没必要再分离最后一个元素，树结构到此到达末端。

时，说明分离后的剩余项的次数为 0，理论上可以继续分离下去，但是实际上并没有必要，到达树的末端。

以 或 为例，可以把树结构可视化为：

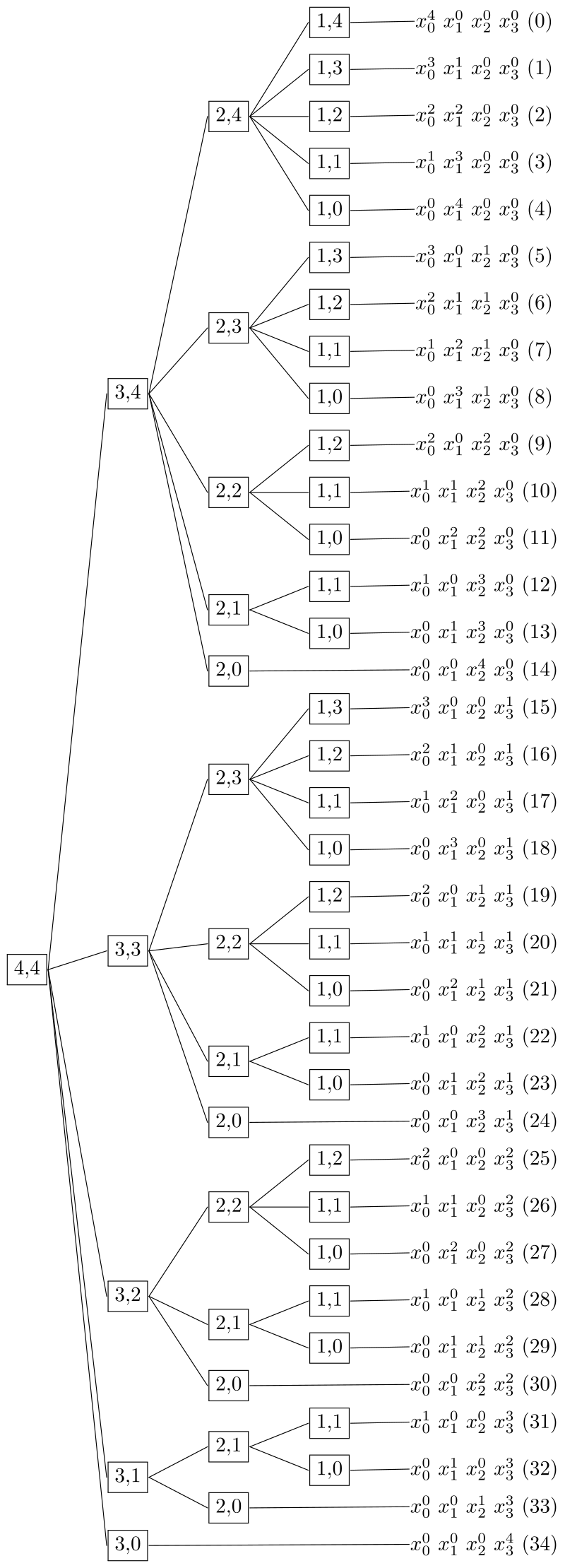
惊喜地发现从上到下末节点的次序和 GRevLex 有一致性。

需要注意的是，在编程实现的时候，每一个子节点并不持有系数数据，而是只持有指针。

索引

这样一套组织严密的网络，使得我们能高效地访问系数。比如我们想索引 的系数。根据分离最后一个元素的原则，分离 后的齐次多项式为 ，于是我们在树结构的第二层找到了 的子节点 ，它位于 的子节点的第 1 位（从 0 计数），序号跟 的次数相同。然后分离 ，分离后的齐次多项式为 ，我们在 的子节点中的第 1 位找到了 。以此类推，仅需 3 次加法（加法计算节点的偏移）即可索引到系数。这相比遍历 GRevLex 有着实质性的优化，属于用空间换时间的生动体现。我们不妨分析一下索引的时间复杂度，对于 ，改进前的时间复杂度为 ，改进后的时间复杂度为 ，当次数 较大时，复杂度明显降低。

遍历

树的遍历一般离不开递归。写一段递归的代码遍历这棵树也比较容易。但是考虑到树的抽象原型是齐次多项式，具有一定的特殊性，有时候也不是非递归不可，比如齐次多项式的数乘，把每个系数都乘以乘数即可，这种情况下直接遍历保存着系数的数组反而效率更高，用不着递归。而且，即便递归，其实遍历到末节点的次序和 GRevLex 也是一模一样的（可以自行验证）。

进阶

我们在对齐次多项式的多叉树表示法进行研究时，并没有止步于此，下面是研究过程中发现的其他有意思的问题：

1. 乘法。把齐次多项式抽象成树，便于索引还只是优点当中的冰山一角，它的真正强大之处在于便于乘法的编程。
2. 一共有多少个子节点？这个结果对于子结点的动态内存分配有意义，进而也能衡量我们在空间方面付出的代价。
3. 我们建模时，思想是分离单项式的最后一个元素，如果分离第一个元素，树的结构有何改变？
4. 齐次多项式的系数一定是常数吗？在抽象代数多项式环的理论中，多项式的系数可以是任何数学实体。但是万变不离其宗，再复杂的表达式我们都可以通过多叉树进行高效的操作。