常值连续推力下航天器的运动
2021-09-25 12:00:00
本文参考了钱学森的论文《Take-off from satellite orbit》和 Battin 的专著《An Introduction to the Mathematics and Methods of Astrodynamics》。
钱学森早在 1953 年就已经研究了常值连续推力下航天器的运动,时隔近七十年,很难再发现这个问题有何新颖之处,不过它所导出的一些数学结果是相当有趣的,而且基于这个问题,也能窥探出解决航天动力学问题所采用的一些解析方法。
极坐标形式的二体相对运动微分方程
已知二体问题的基本微分方程是
在下图中,定义了与航天器固联的一对正交单位向量
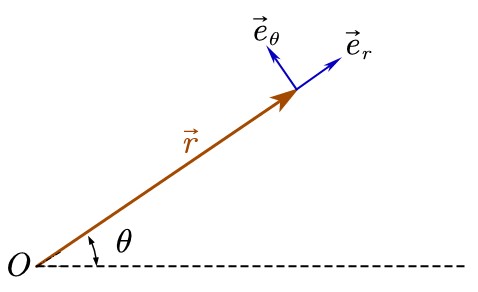
有如下关系
两式左右两边都对时间求导
由于
故
和
观察上式,很容易得到极坐标形式的二体相对运动微分方程
常值连续推力
本文不考虑常值连续推力的工程实际性,只以理想的模型来刻画问题。在下图中,从原点到航天器的方向为径向,与径向垂直的方向为横向。
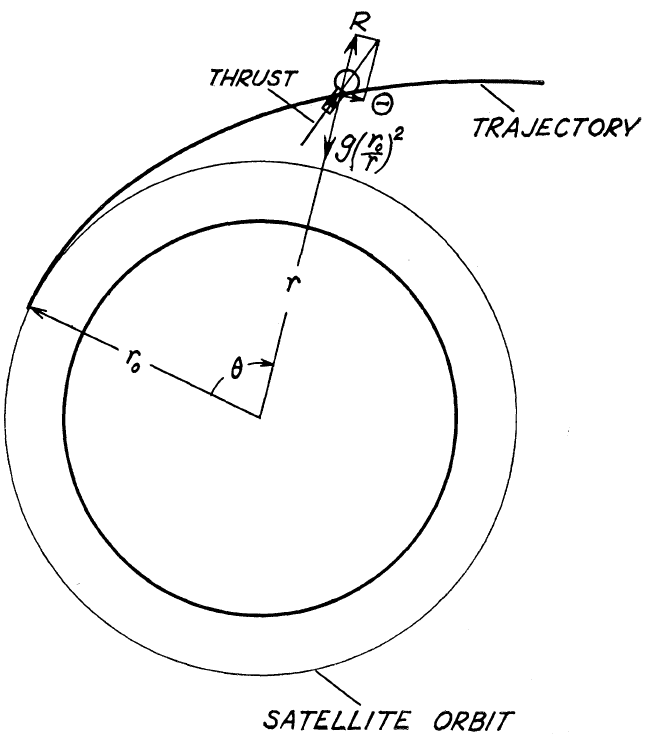
下面将分别研究航天器在径向、横向的常值加速度作用下的运动。分别用
常值径向加速度
假设航天器初始位于半径为
对第二个方程积分,并带入初始条件
把
观察到
结合以上两个式子,不难得到
航天器达到逃逸速度(抛物线速度)满足机械能为
把相关的表达式代入,解出逃逸时的径向距离为
进而把径向速度的平方改写为
我们不希望在逃逸之前径向速度
即
这就是常值径向逃逸加速度所要满足的条件,其中
如果
另外,根据前面
相比七十年前,今天我们可以“作弊”——用数值方法把轨道积分出来。设置初始圆轨道的半径为 8000km,仿真时间 10 小时,系数
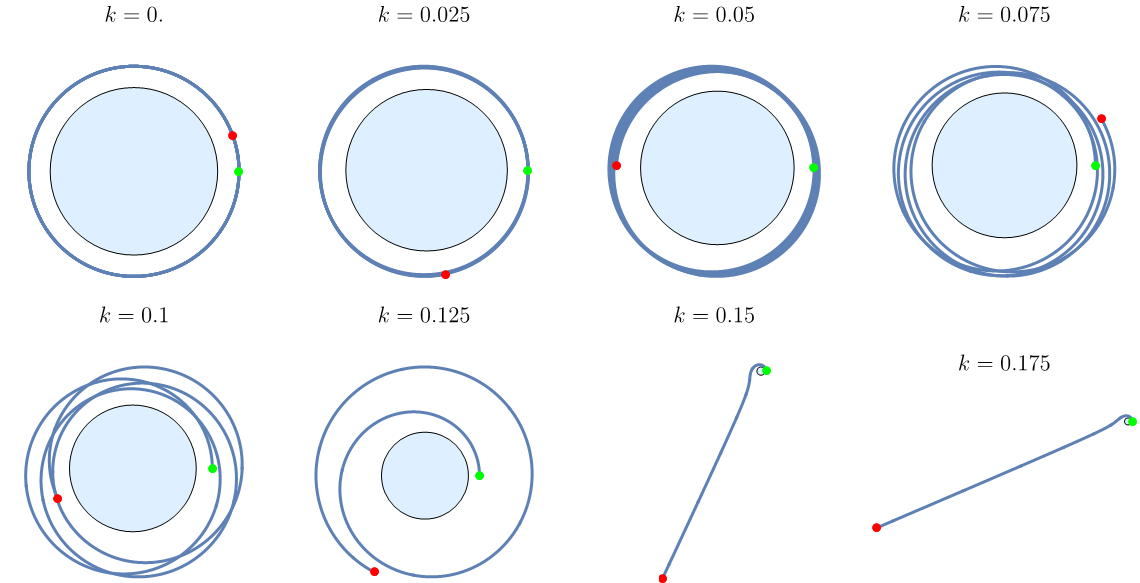
没有达到逃逸条件时,航天器的轨道的确存在一个最大高度。
在钱学森的论文中,逃逸时间
两边积分。但是这个椭圆积分非常难算,感兴趣的读者可以参考 Battin 的专著。
假设
即
把逃逸时间
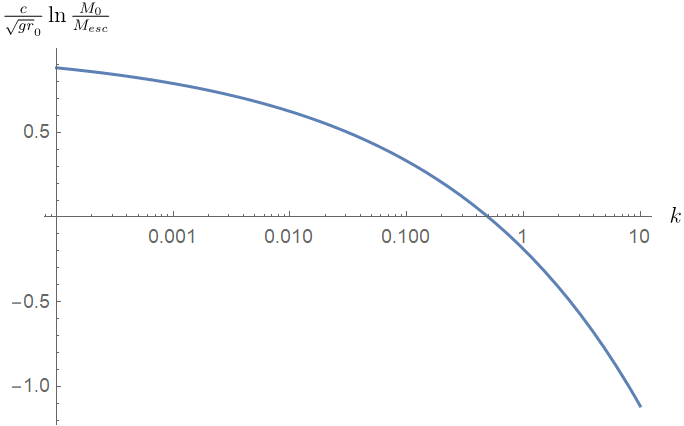
它的图像长下面的样子(这是论文里的原图。说实话,这个曲线我没有复现出来,但是我可以证明它的趋势是对的)
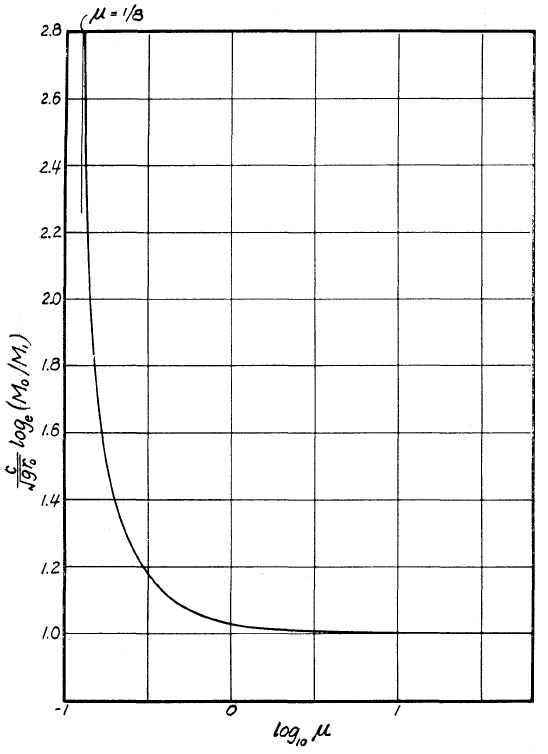
分析曲线的以下特征:
当
当
合 力 向 心 力
推力全部用来维持圆周运动,再没有多余的能量用来增加航天器的总能量,所以航天器直到消耗完所有燃料也始终无法逃逸,即
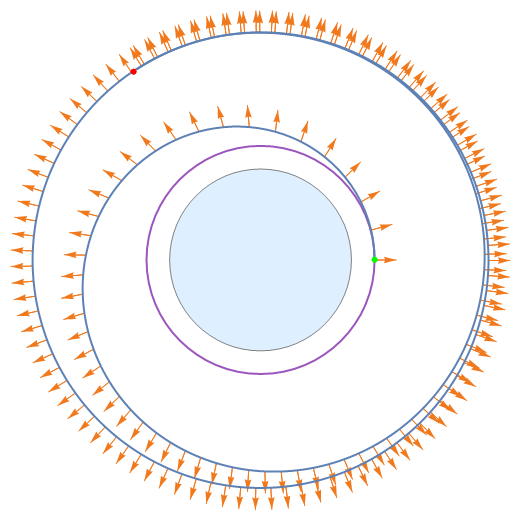
- 当
常值横向加速度
假设航天器初始位于半径为
如果直接在第一个方程中导出
对于很小的横向加速度
代入运动方程的第二个式子,得
即
两边积分,并带入初始条件,得径向距离与时间的关系:
进而
根据运动方程的第一个式子,并根据
把相关的表达式代入逃逸条件
根据径向距离与时间的关系,得到逃逸时间为:
根据
得
整理一下
画出图像
但请不要忘记我们的假设条件:径向加速度很小。在
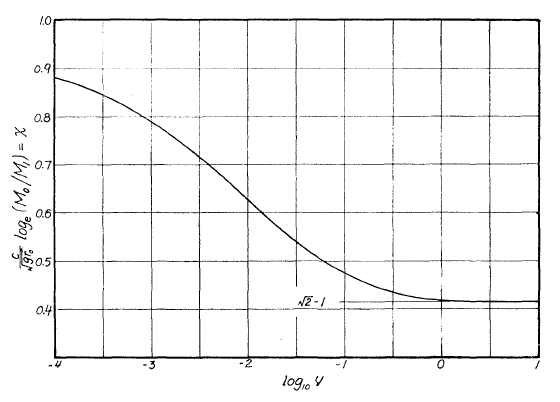
分析曲线的两个特征:
- 当
- 当
用数值方法把轨道计算出来,仿真条件不变,系数
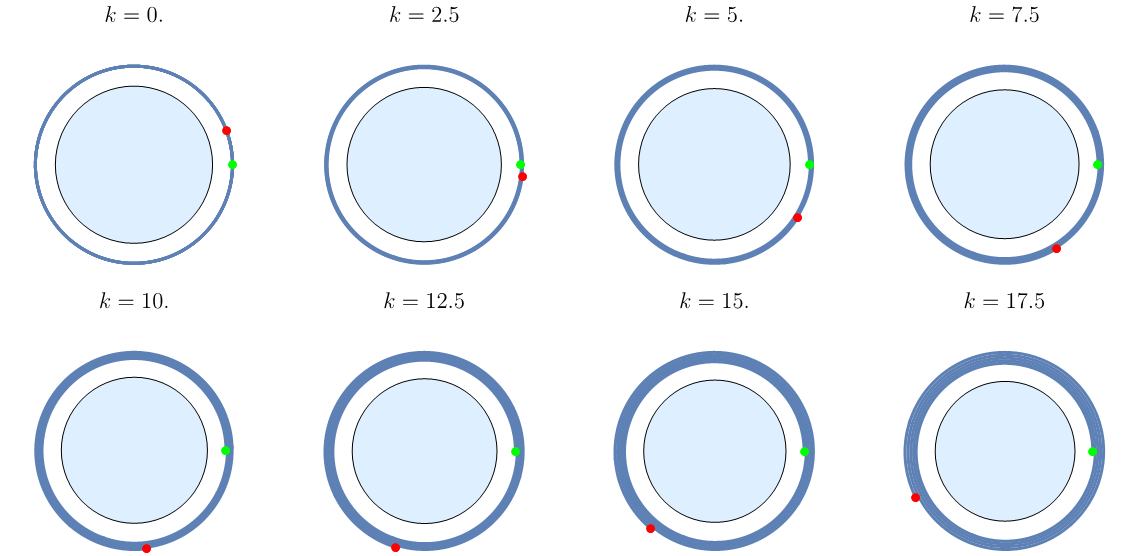
结尾
我个人觉得钱学森的这篇论文的思想很深刻(否则也不会被 Battin 选入教材),处理问题的很多技巧值得学习。
常值连续推力下航天器的运动